


Next: Digression on Real Plane Algebraic
Up: Patchworking Algebraic Curves Disproves the
Previous: Patchworking Algebraic Curves Disproves the
Combinatorial Look on Patchworking
Initial Data.
Let 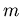 be a positive integer (it
will be the degree of the curve under construction) and
be a positive integer (it
will be the degree of the curve under construction) and 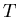 be the
triangle in
be the
triangle in
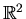 with vertices
with vertices 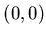 ,
, 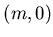 ,
, 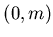 .
Let
.
Let 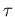 be a triangulation of
be a triangulation of 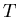 with vertices
having integer coordinates
and equipped with signs. The sign
(plus or minus) at the vertex with coordinates
with vertices
having integer coordinates
and equipped with signs. The sign
(plus or minus) at the vertex with coordinates 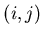 is denoted by
is denoted by
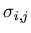 .
.
Construction of Piecewise Linear Curve. Take copies
of 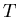 , where
, where
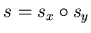 and
and
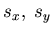 are reflections with respect to the coordinate axes.
Denote by
are reflections with respect to the coordinate axes.
Denote by 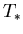 the square
the square
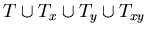 .
Extend the triangulation
.
Extend the triangulation 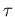 to a symmetric triangulation of
to a symmetric triangulation of 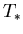 ,
and the distribution of signs
,
and the distribution of signs
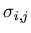 to a distribution at the vertices of the extended triangulation by
the following rule:
to a distribution at the vertices of the extended triangulation by
the following rule:
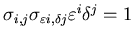 , where
, where
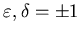 . In other words, passing from a vertex to its
mirror image with respect to an axis we preserve its sign if the
distance from the vertex to the axis is even, and change the sign if
the distance is odd.
. In other words, passing from a vertex to its
mirror image with respect to an axis we preserve its sign if the
distance from the vertex to the axis is even, and change the sign if
the distance is odd.
If a triangle of the triangulation of 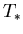 has vertices
of different signs, select a midline separating pluses from minuses.
Denote by
has vertices
of different signs, select a midline separating pluses from minuses.
Denote by 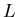 the union of the selected
midlines. It is a collection of polygonal lines contained in
the union of the selected
midlines. It is a collection of polygonal lines contained in 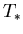 .
The pair
.
The pair 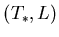 is called the result of affine combinatorial
patchworking. Glue by
is called the result of affine combinatorial
patchworking. Glue by 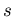 the sides of
the sides of 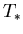 . The resulting space
. The resulting space
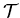 is homeomorphic to the real projective plane
is homeomorphic to the real projective plane
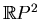 . Denote
by
. Denote
by
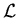 the image of
the image of 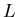 in
in
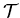 and call the pair
and call the pair
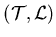 the result of projective combinatorial patchworking.
the result of projective combinatorial patchworking.
Figure 1:
Initial data and the result of combinatorial patchworking of
it.
 |
Let us introduce an additional assumption:
the triangulation 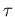 of
of 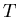 is
convex. This means that
there exists a convex
piecewise-linear function
is
convex. This means that
there exists a convex
piecewise-linear function
 which is linear on each triangle of
which is linear on each triangle of 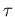 and
not linear on the union of any two triangles of
and
not linear on the union of any two triangles of 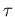 .
.
1 (Patchwork Theorem)
Under the assumptions above on the triangulation
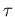
of
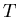
, there exist a
nonsingular real algebraic plane affine curve of
degree
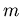
and a homeomorphism of the plane
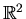
onto the interior of the square
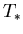
mapping the set of real points of
this curve onto
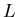
. Furthermore, there exists a homeomorphism
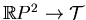
mapping the set of real points of the corresponding
projective curve onto
.
Figure 2:
Patchwork of a counter-example to Ragsdale Conjecture
with degree 10 and p=32.
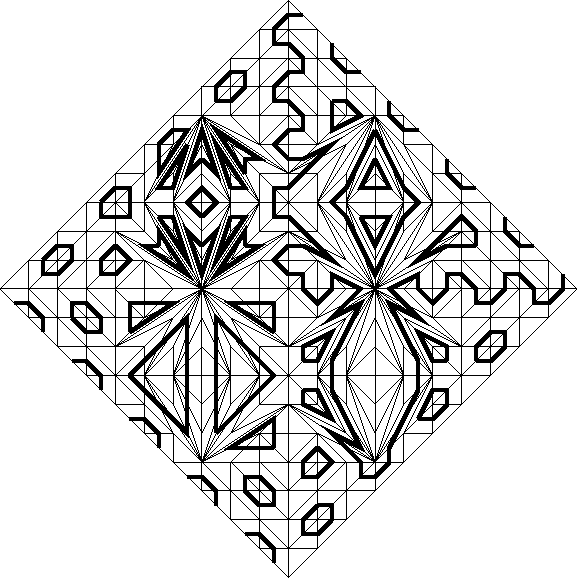 |
Figure 3:
Patchwork of a counter-example to Ragsdale Conjecture
with degree 10 and n=32.
 |



Next: Digression on Real Plane Algebraic
Up: Patchworking Algebraic Curves Disproves the
Previous: Patchworking Algebraic Curves Disproves the
2002-11-16
![]() be a positive integer (it
will be the degree of the curve under construction) and
be a positive integer (it
will be the degree of the curve under construction) and ![]() be the
triangle in
be the
triangle in
![]() with vertices
with vertices ![]() ,
, ![]() ,
, ![]() .
Let
.
Let ![]() be a triangulation of
be a triangulation of ![]() with vertices
having integer coordinates
and equipped with signs. The sign
(plus or minus) at the vertex with coordinates
with vertices
having integer coordinates
and equipped with signs. The sign
(plus or minus) at the vertex with coordinates ![]() is denoted by
is denoted by
![]() .
.
![]() has vertices
of different signs, select a midline separating pluses from minuses.
Denote by
has vertices
of different signs, select a midline separating pluses from minuses.
Denote by ![]() the union of the selected
midlines. It is a collection of polygonal lines contained in
the union of the selected
midlines. It is a collection of polygonal lines contained in ![]() .
The pair
.
The pair ![]() is called the result of affine combinatorial
patchworking. Glue by
is called the result of affine combinatorial
patchworking. Glue by ![]() the sides of
the sides of ![]() . The resulting space
. The resulting space
![]() is homeomorphic to the real projective plane
is homeomorphic to the real projective plane
![]() . Denote
by
. Denote
by
![]() the image of
the image of ![]() in
in
![]() and call the pair
and call the pair
![]() the result of projective combinatorial patchworking.
the result of projective combinatorial patchworking.
![]() of
of ![]() is
convex. This means that
there exists a convex
piecewise-linear function
is
convex. This means that
there exists a convex
piecewise-linear function
![]() which is linear on each triangle of
which is linear on each triangle of ![]() and
not linear on the union of any two triangles of
and
not linear on the union of any two triangles of ![]() .
.