References beginning with D
 O. T. Dasbach,
On subspaces of the space of Vassiliev invariants,
Düsseldorf University thesis, August 1995.
O. T. Dasbach,
On subspaces of the space of Vassiliev invariants,
Düsseldorf University thesis, August 1995.
 O. T. Dasbach,
A remark on the HOMFLY-Vassiliev invariants,
Düsseldorf University preprint, October 1996.
O. T. Dasbach,
A remark on the HOMFLY-Vassiliev invariants,
Düsseldorf University preprint, October 1996.
 O. T. Dasbach,
On the combinatorial structure of primitive Vassiliev
invariants II,
Jour. Comb. Theory, Ser. A, to appear.
O. T. Dasbach,
On the combinatorial structure of primitive Vassiliev
invariants II,
Jour. Comb. Theory, Ser. A, to appear.
 O. T. Dasbach,
On the combinatorial structure of primitive Vassiliev invariants III
-- a lower bound,
Comm. in Cont. Math. 2-4 (2000) 579-590,
arXiv:math.GT/9806086.
O. T. Dasbach,
On the combinatorial structure of primitive Vassiliev invariants III
-- a lower bound,
Comm. in Cont. Math. 2-4 (2000) 579-590,
arXiv:math.GT/9806086.
 O. T. Dasbach and X-S. Lin,
The Bennequin number of n-trivial closed n-braids is negative,
University of California at Riverside preprint, October 2000,
arXiv:math.GT/0010278.
O. T. Dasbach and X-S. Lin,
The Bennequin number of n-trivial closed n-braids is negative,
University of California at Riverside preprint, October 2000,
arXiv:math.GT/0010278.
 C. Day,
Vassiliev invariants for links,
Univ. of North Carolina at Chapel Hill preprint, 1992.
C. Day,
Vassiliev invariants for links,
Univ. of North Carolina at Chapel Hill preprint, 1992.
 J. Dean,
Many classical knot invariants are not Vassiliev invariants,
Jour. of Knot Theory and its Ramifications, 3(1) (1994) 7-9.
J. Dean,
Many classical knot invariants are not Vassiliev invariants,
Jour. of Knot Theory and its Ramifications, 3(1) (1994) 7-9.
 C. De Concini and C. Procesi,
Hyperplane arrangements and holonomy equations,
Selecta Math., to appear.
C. De Concini and C. Procesi,
Hyperplane arrangements and holonomy equations,
Selecta Math., to appear.
 T. Deguchi and K. Tsurusaki,
A statistical study of random knotting using the Vassiliev invariants,
Jour. of Knot Theory and its Ramifications 3(3) (1994) 321-353.
T. Deguchi and K. Tsurusaki,
A statistical study of random knotting using the Vassiliev invariants,
Jour. of Knot Theory and its Ramifications 3(3) (1994) 321-353.
 T. Deguchi and K. Tsurusaki,
Numerical application of knot invariants and universality of random
knotting,
in Knot theory (V. F. R. Jones, J. Kania-Bartoszynska,
J. H. Przytycki, P. Traczyk, and V. G. Turaev, eds.), Banach Center
Publications 42 77-85, Warsaw 1998.
T. Deguchi and K. Tsurusaki,
Numerical application of knot invariants and universality of random
knotting,
in Knot theory (V. F. R. Jones, J. Kania-Bartoszynska,
J. H. Przytycki, P. Traczyk, and V. G. Turaev, eds.), Banach Center
Publications 42 77-85, Warsaw 1998.
 C. Di Bartolo,
R. Gambini, J. Griego and J. Pullin,
Consistent canonical quantization of general relativity in the
space of Vassiliev knot invariants,
gr-qc/9909063 preprint,
September 1999.
C. Di Bartolo,
R. Gambini, J. Griego and J. Pullin,
Consistent canonical quantization of general relativity in the
space of Vassiliev knot invariants,
gr-qc/9909063 preprint,
September 1999.
 C. Di Bartolo,
R. Gambini, J. Griego and J. Pullin,
Canonical quantum gravity in the Vassiliev invariants arena: I.
Kinematical structure,
preprint, November 1999,
arXiv:gr-qc/9911009.
C. Di Bartolo,
R. Gambini, J. Griego and J. Pullin,
Canonical quantum gravity in the Vassiliev invariants arena: I.
Kinematical structure,
preprint, November 1999,
arXiv:gr-qc/9911009.
 C. Di Bartolo,
R. Gambini, J. Griego and J. Pullin,
Canonical quantum gravity in the Vassiliev invariants arena: II.
Constraints, habitats and consistency of the constraint algebra,
preprint, November 1999,
arXiv:gr-qc/9911010.
C. Di Bartolo,
R. Gambini, J. Griego and J. Pullin,
Canonical quantum gravity in the Vassiliev invariants arena: II.
Constraints, habitats and consistency of the constraint algebra,
preprint, November 1999,
arXiv:gr-qc/9911010.
 Tudor Dimofte, Sergei Gukov, Jonatan Lenells, Don
Zagier,
Exact Results for Perturbative Chern-Simons Theory with Complex Gauge
Group.
http://arxiv.org/abs/0903.2472
Tudor Dimofte, Sergei Gukov, Jonatan Lenells, Don
Zagier,
Exact Results for Perturbative Chern-Simons Theory with Complex Gauge
Group.
http://arxiv.org/abs/0903.2472
 M. Domergue and P. Donato,
Integrating a weight system of order
M. Domergue and P. Donato,
Integrating a weight system of order 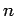 to an invariant of
to an invariant of
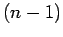 -singular knots,
Jour. of Knot Theory and its Ramifications, 5(1) (1996) 23-35.
-singular knots,
Jour. of Knot Theory and its Ramifications, 5(1) (1996) 23-35.
 S. Duzhin
, Lectures on the Vassiliev knot
invariants. Lectures in Mathematical Sciences, The University of Tokyo,
vol. 19, 2002. 123 pp.
http://www.pdmi.ras.ru/~duzhin/Vics/vics.ps.gz.
S. Duzhin
, Lectures on the Vassiliev knot
invariants. Lectures in Mathematical Sciences, The University of Tokyo,
vol. 19, 2002. 123 pp.
http://www.pdmi.ras.ru/~duzhin/Vics/vics.ps.gz.
 S. Duzhin,
Conway polynomial and Magnus expansion.
http://arxiv.org/abs/1001.2500
S. Duzhin,
Conway polynomial and Magnus expansion.
http://arxiv.org/abs/1001.2500
 S. Duzhin and M.Karev,
Detecting the orientation of long links by finite type invariants
. Preprint, July 1, 2005.
http://www.pdmi.ras.ru/~duzhin/papers/,
arXiv:math.GT/0507015.
S. Duzhin and M.Karev,
Detecting the orientation of long links by finite type invariants
. Preprint, July 1, 2005.
http://www.pdmi.ras.ru/~duzhin/papers/,
arXiv:math.GT/0507015.
 I. Dynnikov,
The Alexander polynomial in several variables can be expressed in terms of
the Vassiliev invariants.
Russian Mathematical Surveys, 1997, 52:1, 219-221.
I. Dynnikov,
The Alexander polynomial in several variables can be expressed in terms of
the Vassiliev invariants.
Russian Mathematical Surveys, 1997, 52:1, 219-221.
Sergei DUZHIN
2013-07-04