References beginning with S
 J. Sawada,
A fast algorithm for generating non-isomorphic chord diagrams,
SIAM Jour. on Discrete Math., 15-4 (2002) 546-561.
J. Sawada,
A fast algorithm for generating non-isomorphic chord diagrams,
SIAM Jour. on Discrete Math., 15-4 (2002) 546-561.
 S. F. Sawin,
Primitive Vassiliev invariants,
MIT preprint, April 1993.
S. F. Sawin,
Primitive Vassiliev invariants,
MIT preprint, April 1993.
 S. F. Sawin,
Finite-degree link invariants and connectivity,
Jour. of Knot Theory and its Ramifications 5(1) (1996) 117-136.
S. F. Sawin,
Finite-degree link invariants and connectivity,
Jour. of Knot Theory and its Ramifications 5(1) (1996) 117-136.
 J. Sawollek,
An orientation-sensitive Vassiliev invariant for virtual knots,
Universität Dortmund preprint, March 200, arXiv:math.GT/0203123.
J. Sawollek,
An orientation-sensitive Vassiliev invariant for virtual knots,
Universität Dortmund preprint, March 200, arXiv:math.GT/0203123.
 J. Sawon,
Rozansky-Witten invariants of hyperKähler manifolds,
Ph.D. thesis, University of Cambridge, October 1999.
J. Sawon,
Rozansky-Witten invariants of hyperKähler manifolds,
Ph.D. thesis, University of Cambridge, October 1999.
 J. Sawon,
The Rozansky-Witten invariants of hyperKähler manifolds,
Proceedings of the 7th International Conference on Differential Geometry
and Applications, Brno, August 1998.
J. Sawon,
The Rozansky-Witten invariants of hyperKähler manifolds,
Proceedings of the 7th International Conference on Differential Geometry
and Applications, Brno, August 1998.
 J. Sawon,
A new weight system on chord diagrams via hyperkähler geometry,
Proceedings of the Second Meeting on Quaternionic Structures in
Mathematics and Physics, Roma, September 1999,
arXiv:math.DG/0002218.
J. Sawon,
A new weight system on chord diagrams via hyperkähler geometry,
Proceedings of the Second Meeting on Quaternionic Structures in
Mathematics and Physics, Roma, September 1999,
arXiv:math.DG/0002218.
 J. Sawon,
Topological quantum field theory and hyperKhler geometry,
Proceedings of the 7th Gökova Geometry-Topology Conference and Turk.
J. Math. 25 (2001) 169-194, arXiv:math.QA/0009222.
J. Sawon,
Topological quantum field theory and hyperKhler geometry,
Proceedings of the 7th Gökova Geometry-Topology Conference and Turk.
J. Math. 25 (2001) 169-194, arXiv:math.QA/0009222.
 J. Sawon,
When is a Lie algebra not a Lie algebra?
Proceedings of the IXth Oporto Meeting on Geometry, Topology & Physics,
September-October 2000.
J. Sawon,
When is a Lie algebra not a Lie algebra?
Proceedings of the IXth Oporto Meeting on Geometry, Topology & Physics,
September-October 2000.
 R. Schneiderman,
Algebraic linking numbers of knots in 3-manifolds,
Algebraic and Geometric Topology 3-31 (2003) 921-968,
arXiv:math.GT/0202024.
R. Schneiderman,
Algebraic linking numbers of knots in 3-manifolds,
Algebraic and Geometric Topology 3-31 (2003) 921-968,
arXiv:math.GT/0202024.
 R. Schneiderman,
Simple Whitney towers, half-gropes and the Arf invariant of a
knot,
New York University preprint, October 2003, arXiv:math.GT/0310304.
R. Schneiderman,
Simple Whitney towers, half-gropes and the Arf invariant of a
knot,
New York University preprint, October 2003, arXiv:math.GT/0310304.
 R. Schneiderman and P. Teichner,
Whitney towers and the Kontsevich integral,
Proceedings of the Casson fest, Geometry and
Topology Monographs 7 101-134, arXiv:math.GT/0401441.
R. Schneiderman and P. Teichner,
Whitney towers and the Kontsevich integral,
Proceedings of the Casson fest, Geometry and
Topology Monographs 7 101-134, arXiv:math.GT/0401441.
 K. Selwat,
Niezmienniki Vassilieva krzywych na plaszczyznie,
University of Wroclaw Master's thesis, 1995.
K. Selwat,
Niezmienniki Vassilieva krzywych na plaszczyznie,
University of Wroclaw Master's thesis, 1995.
 K. Selwat,
The first order semilocal Vassiliev invariants of plane curves,
Jour. of Knot Theory and its Ramifications 7(8) (1998).
K. Selwat,
The first order semilocal Vassiliev invariants of plane curves,
Jour. of Knot Theory and its Ramifications 7(8) (1998).
 N. Shirokova,
The space of 3-manifolds and Vassiliev finite-type invariants,
University of Chicago preprint, May 1997. See also
q-alg/9705008.
N. Shirokova,
The space of 3-manifolds and Vassiliev finite-type invariants,
University of Chicago preprint, May 1997. See also
q-alg/9705008.
 N. Shirokova,
On the classification of Floer-type theories,
arXiv:0704.1330.
N. Shirokova,
On the classification of Floer-type theories,
arXiv:0704.1330.
 A. Shumakovitch,
Shadow formula for the Vassiliev invariant of degree two,
Topology 36-2 (1997).
A. Shumakovitch,
Shadow formula for the Vassiliev invariant of degree two,
Topology 36-2 (1997).
 D. J. Sinha,
The topology of spaces of knots,
Brown University preprint, February 2002, arXiv:math.AT/0202287.
D. J. Sinha,
The topology of spaces of knots,
Brown University preprint, February 2002, arXiv:math.AT/0202287.
 D. Sinha, Operads and Knot Spaces, preprint.
D. Sinha, Operads and Knot Spaces, preprint.
 S. A. Sirotine,
Approximation of knot invariants by Vassiliev invariants,
Rice University preprint, April 1995.
S. A. Sirotine,
Approximation of knot invariants by Vassiliev invariants,
Rice University preprint, April 1995.
 C. T. Snydal,
Vassiliev knot invariants arising from the Lie superalgebra
C. T. Snydal,
Vassiliev knot invariants arising from the Lie superalgebra
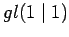 ,
University of North Carolina physics undergraduate thesis, May 1995.
,
University of North Carolina physics undergraduate thesis, May 1995.
 E. Soboleva,
Vassiliev knot invariants coming from Lie algebras and
4-invariants,
Jour. of Knot Theory and its Ramifications 10(1) (2001).
E. Soboleva,
Vassiliev knot invariants coming from Lie algebras and
4-invariants,
Jour. of Knot Theory and its Ramifications 10(1) (2001).
 A. B. Sossinsky,
Feynman diagrams and Vassiliev invariants,
IHES preprint IHES/M/92/13, February 1992.
A. B. Sossinsky,
Feynman diagrams and Vassiliev invariants,
IHES preprint IHES/M/92/13, February 1992.
 T. Stanford,
Finite type invariants of knots, links, and graphs,
Topology 35-4 (1996) 1027-1050.
T. Stanford,
Finite type invariants of knots, links, and graphs,
Topology 35-4 (1996) 1027-1050.
 T. Stanford,
Braid commutators and Vassiliev invariants,
Pacific Jour. of Math. 174-1 (1996).
T. Stanford,
Braid commutators and Vassiliev invariants,
Pacific Jour. of Math. 174-1 (1996).
 T. Stanford,
The functoriality of Vassiliev-type invariants of links,
braids, and knotted graphs,
Jour. of Knot Theory and its Ramifications 3(3) (1994)
247-262.
T. Stanford,
The functoriality of Vassiliev-type invariants of links,
braids, and knotted graphs,
Jour. of Knot Theory and its Ramifications 3(3) (1994)
247-262.
 T. Stanford,
Computing Vassiliev's invariants,
Topology and its Applications 77-3 (1997). See also programs at
ftp://geom.umn.edu/pub/contrib/vassiliev.tar.Z.
T. Stanford,
Computing Vassiliev's invariants,
Topology and its Applications 77-3 (1997). See also programs at
ftp://geom.umn.edu/pub/contrib/vassiliev.tar.Z.
 T. Stanford,
Vassiliev invariants and knots modulo pure braid subgroups,
United States Naval Academy preprint, May 1998, arXiv:math.GT/9805092.
T. Stanford,
Vassiliev invariants and knots modulo pure braid subgroups,
United States Naval Academy preprint, May 1998, arXiv:math.GT/9805092.
 T. Stanford,
Four observations on
T. Stanford,
Four observations on 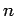 -triviality and Brunnian links,
United States Naval Academy preprint, July 1998. See also
math.GT/9807161.
-triviality and Brunnian links,
United States Naval Academy preprint, July 1998. See also
math.GT/9807161.
 T. Stanford,
Braid commutators and delta finite-type invariants,
United States Naval Academy preprint, July 1999. See also
math.GT/9907071.
T. Stanford,
Braid commutators and delta finite-type invariants,
United States Naval Academy preprint, July 1999. See also
math.GT/9907071.
 T. Stanford,
Some computational results on mod 2 finite-type invariants of
knots and string links,
Invariants of knots and 3-manifolds (Kyoto 2001), Geometry and
Topology Monographs 4 363-376.
T. Stanford,
Some computational results on mod 2 finite-type invariants of
knots and string links,
Invariants of knots and 3-manifolds (Kyoto 2001), Geometry and
Topology Monographs 4 363-376.
 T. Stanford and R. Trapp,
On knot invariants which are not of finite type,
United States Naval Academy and California State University (San
Bernardino) preprint, March 1999. See also
math.GT/9903057.
T. Stanford and R. Trapp,
On knot invariants which are not of finite type,
United States Naval Academy and California State University (San
Bernardino) preprint, March 1999. See also
math.GT/9903057.
 A. Stoimenow,
On Harrison cohomology and a conjecture by Drinfel'd,
diploma thesis, Humboldt University, Berlin, 1995 (also available
in German as Über Harrison-kohomologie und die
Drinfel'd-vermutung).
A. Stoimenow,
On Harrison cohomology and a conjecture by Drinfel'd,
diploma thesis, Humboldt University, Berlin, 1995 (also available
in German as Über Harrison-kohomologie und die
Drinfel'd-vermutung).
 A. Stoimenow,
Stirling numbers, Eulerian idempotents and a diagram complex,
version 27/07/2005, published in J. Of Knot Theory and Its Ram.
7(2) (1998), 231-256.
A. Stoimenow,
Stirling numbers, Eulerian idempotents and a diagram complex,
version 27/07/2005, published in J. Of Knot Theory and Its Ram.
7(2) (1998), 231-256.
 A. Stoimenow,
On the number of chord diagrams,
Discr. Math. 218 (2000), 209-233.
(based on a preprint, January 1996).
A. Stoimenow,
On the number of chord diagrams,
Discr. Math. 218 (2000), 209-233.
(based on a preprint, January 1996).
 A. Stoimenow,
Enumeration of chord diagrams and an upper bound for Vassiliev
invariants,
Jour. of Knot Theory and its Ramifications 7(1) (1998) 94-114.
A. Stoimenow,
Enumeration of chord diagrams and an upper bound for Vassiliev
invariants,
Jour. of Knot Theory and its Ramifications 7(1) (1998) 94-114.
 A. Stoimenow,
On enumeration of chord diagrams and asymptotics of Vassiliev
invariants,
PhD thesis, Humboldt University, Berlin, 1999.
A. Stoimenow,
On enumeration of chord diagrams and asymptotics of Vassiliev
invariants,
PhD thesis, Humboldt University, Berlin, 1999.
 A. Stoimenow,
Positive knots, closed braids and the Jones polynomial,
Ann. Scuola Norm. Sup. Pisa Cl. Sci. 2(2) (2003), 237-285.
(previous versions: Humboldt University preprint, May 1997, and
math.GT/9805078).
A. Stoimenow,
Positive knots, closed braids and the Jones polynomial,
Ann. Scuola Norm. Sup. Pisa Cl. Sci. 2(2) (2003), 237-285.
(previous versions: Humboldt University preprint, May 1997, and
math.GT/9805078).
 A. Stoimenow,
Gauss sum invariants, Vassiliev invariants and braiding
sequences,
J. Of Knot Theory and Its Ram. 9(2) (2000), 221-269
(first appeared as a preprint, Humboldt University, May 1997).
A. Stoimenow,
Gauss sum invariants, Vassiliev invariants and braiding
sequences,
J. Of Knot Theory and Its Ram. 9(2) (2000), 221-269
(first appeared as a preprint, Humboldt University, May 1997).
 A. Stoimenow,
The braid index and the growth of Vassiliev invariants
Jour. of Knot Theory and its Ramifications, 8(6) (1999), 799-813.
A. Stoimenow,
The braid index and the growth of Vassiliev invariants
Jour. of Knot Theory and its Ramifications, 8(6) (1999), 799-813.
 A. Stoimenow,
Vassiliev invariants on fibered and mutually obverse knots,
Jour. of Knot Theory and its Ramifications 8(4) (1999) 511-519.
A. Stoimenow,
Vassiliev invariants on fibered and mutually obverse knots,
Jour. of Knot Theory and its Ramifications 8(4) (1999) 511-519.
 A. Stoimenow,
On finiteness of Vassiliev invariants and a proof of the Lin-Wang
conjecture via braiding polynomials,
J. Of Knot Theory and Its Ram. 10(5) (2001),
special volume for the proceedings of the International
Conference on Knot Theory `Knots in Hellas, 98'', 769-780.
A. Stoimenow,
On finiteness of Vassiliev invariants and a proof of the Lin-Wang
conjecture via braiding polynomials,
J. Of Knot Theory and Its Ram. 10(5) (2001),
special volume for the proceedings of the International
Conference on Knot Theory `Knots in Hellas, 98'', 769-780.
 A. Stoimenow,
Genera of knots and Vassiliev invariants,
Jour. of Knot Theory and its Ramifications 8(2) (1999) 253-259.
A. Stoimenow,
Genera of knots and Vassiliev invariants,
Jour. of Knot Theory and its Ramifications 8(2) (1999) 253-259.
 A. Stoimenow,
Gauss sums on almost positive knots,
math.GT/9803073.
Compositio Mathematica 140(1) (2004), 228-254.
A. Stoimenow,
Gauss sums on almost positive knots,
math.GT/9803073.
Compositio Mathematica 140(1) (2004), 228-254.
 A. Stoimenow,
Mutant links distinguished by degree 3 Gauss sums,
(online version: 27/04/1998),
Proceedings of the International Conference on Knot Theory
"Knots in Hellas, 98", Series on Knots and Everything 24, World Scientific,
2000.
A. Stoimenow,
Mutant links distinguished by degree 3 Gauss sums,
(online version: 27/04/1998),
Proceedings of the International Conference on Knot Theory
"Knots in Hellas, 98", Series on Knots and Everything 24, World Scientific,
2000.
 A. Stoimenow,
Some minimal degree Vassiliev invariants not realizable by the
HOMFLY and Kauffman polynomial,
math.GT/9807076.
C. R. Acad. Bulgare Sci. 54(4) (2001), 9-14.
A. Stoimenow,
Some minimal degree Vassiliev invariants not realizable by the
HOMFLY and Kauffman polynomial,
math.GT/9807076.
C. R. Acad. Bulgare Sci. 54(4) (2001), 9-14.
 A. Stoimenow,
Knots of genus one,
Proc. Amer. Math. Soc. 129(7) (2001), 2141-2156
(first appeared as a preprint, Munich, 1998).
A. Stoimenow,
Knots of genus one,
Proc. Amer. Math. Soc. 129(7) (2001), 2141-2156
(first appeared as a preprint, Munich, 1998).
 A. Stoimenow,
A survey on Vassiliev invariants for knots,
Mathematics and Education in Mathematics, Proceedings of 27th Spring
Conference of the Union of Bulgarian Mathematicians, Pleven 1998.
A. Stoimenow,
A survey on Vassiliev invariants for knots,
Mathematics and Education in Mathematics, Proceedings of 27th Spring
Conference of the Union of Bulgarian Mathematicians, Pleven 1998.
 A. Stoimenow,
Vassiliev invariants and rational knots of unknotting number one,
math.GT/9909050.
Topology 42(1) (2003), 227-241.
A. Stoimenow,
Vassiliev invariants and rational knots of unknotting number one,
math.GT/9909050.
Topology 42(1) (2003), 227-241.
 A. Stoimenow,
Polynomial and polynomially growing knot invariants,
Preprint, current version 28/06/2005.
A. Stoimenow,
Polynomial and polynomially growing knot invariants,
Preprint, current version 28/06/2005.
 A. Stoimenow,
The Conway Vassiliev invariants on twist knots,
Kobe J. Math. 16(2) (1999), 189-193.
A. Stoimenow,
The Conway Vassiliev invariants on twist knots,
Kobe J. Math. 16(2) (1999), 189-193.
 A. Stoimenow,
On cabled knots and Vassiliev invariants (not)
contained in knot polynomials,
to appear in Canadian J. Math.
A. Stoimenow,
On cabled knots and Vassiliev invariants (not)
contained in knot polynomials,
to appear in Canadian J. Math.
 A. Stoimenow,
Some applications of Tristram-Levine signatures,
Advances in Mathematics 194(2) (2005), 463-484.
A. Stoimenow,
Some applications of Tristram-Levine signatures,
Advances in Mathematics 194(2) (2005), 463-484.
 Y. Suetsugu,
Kontsevich invariant for links in a donut and links of satellite
form,
Osaka J. of Math. 33 (1996) 823-828.
Y. Suetsugu,
Kontsevich invariant for links in a donut and links of satellite
form,
Osaka J. of Math. 33 (1996) 823-828.
Sergei DUZHIN
2013-07-04