A Dozen Low-dimensional Problems

compiled and typeset by S. V. Duzhin
October 5, 2001

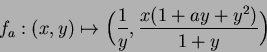
Problem 1. (M. Shapiro) A rational periodic map.


Prove that the rational mapping of the plane into itself defined as

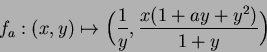
\begin{displaymath} f_a: (x,y) \mapsto \Bigl(\frac{1}{y},\frac{x(1+ay+y^2)}{1+y}\Bigr) \end{displaymath}

is periodic only for $a=2$.

If $a=2$, then we get a mapping $f(x,y)=(1/y,x(1+y))$ that has period 5, i.e. $f^5=\mathop{\rm id}\nolimits $. Explain the reason why. For example, note that the positive quadrant $Q=\{x>0,y>0\}$ is stable under $f$ and $f$ has exactly one fixed point in $Q$. Is it true that there is a diffeomorphism $\varphi :Q\to D$, where $D$ is the open unit disk, such that $\varphi \circ f= r_5\circ\varphi $, where $r_5$ is rotation through $72^\circ$.

Figure: Periodic rational map $f:\mathbb R^2\to\mathbb R^2$
\begin{figure}\begin{center} \epsfxsize 12cm \epsfbox{per5.eps}\end{center}\end{figure}

Is it true in general that a periodic mapping of a disk with one fixed point is equivalent to a rotation?


Problem 2. (B. Shapiro) Roots of a complex polynomial and its derivative and doubly stochastic matrices.


(A) Let $P$ be a complex polynomial of degree $n$ and $A=(a_1,...,a_n)$ the vector of its roots (in arbitrary order). We construct a new vector $B=(b_1,...,b_{n-1},\beta)$, where $b_1$, ..., $b_{n-1}$ are the roots of the derivative $P'$ and $\beta=\sum a_i/n =\sum b_j/(n-1)$. Since the roots of the derivative lie inside the convex hull of initial roots $a_i$, there is a row-stochastic matrix $M$ with last row $1/n,1/n,...,1/n$ such that

\begin{displaymath} B=MA, \end{displaymath}

where $A$ and $B$ are understood as column vectors. A row-stochastic matrix consists of non-negative numbers the sum of which in every row is 1.

If n>3, then the choice of such matrix $M$ is not unique. The question is whether it is possible to choose it among doubly stochastic matrices (such that the sums in every column are also 1).


(B) Problem (A) has the following generalization to an arbitrary dimension $k$ ($k=2$ corresponds to the case of point sets in the plane $\mathbb{C}$ considered above).


Definition 1. Given an unordered $n$-tuple $V$ of vectors (points) $(v_1,...,v_n)$ in $\mathbb{R}^k$ let us denote by $\mathop{\rm Pol}\nolimits (V)$ the polytope in $\mathop{\rm Mat}\nolimits (n,k)$ obtained as follows. (Here $\mathop{\rm Mat}\nolimits (n,k)$ is the space of real $n\times k$-matrices and we assume $k\le n$). For each ordering $i_1,...,i_n$ of the given vectors we get a matrix in $\mathop{\rm Mat}\nolimits (n,k)$ with the rows $v_{i_1},...,v_{i_n}$. Take the convex hull of all these $n!$ matrices and call it $\mathop{\rm Pol}\nolimits (V)$.


Definition 2. An unordered $n$-tuple $V$ of vectors in $\mathbb{R}^k$ is said to be wider than another such $n$-tuple $W$ if $\mathop{\rm Pol}\nolimits (W)$ is contained in $\mathop{\rm Pol}\nolimits (V)$.


Definition 3. Given an $n$-tuple $V$ of unordered vectors in $\mathbb{R}^k$ we call its derived $n$-tuple $\mathop{\rm Der}\nolimits (V)$ the following thing. Let us place unit electric charges at each point $v_1$, ..., $v_n$ and consider their common electrostatic field

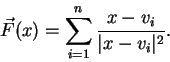
\begin{displaymath} \vec{F}(x)=\sum_{i=1}^n\frac{x-v_i}{\vert x-v_i\vert^2}. \end{displaymath}

There exist $n-1$ points (counting with multiplicities) where this field vanishes. Add the meanvalue $\sum_i v_i/n$ to this $(n-1)$-tuple and you get $\mathop{\rm Der}\nolimits (V)$.


Conjecture. Any finite point set $V$ is wider than its derivative $\mathop{\rm Der}\nolimits (V)$.


For $k=1$ the proof is easy. The case $k=2$ coincides with Problem A above since the zeros of the electrostatic field coincide with the zeros of the derivative of the polynomial in 1 complex variable whose roots are given points on $\mathbb{C}$.


Problem 3. (O.Oestlund) Untangling plane curves without second Reidemeister move.


Let $\Omega _1$, $\Omega _2$, $\Omega _3$ be Reidemeister moves considered in the class of generic immersed plane curves (plane curves that may have only transversal double points as singularities):

$\Omega _1$ (cusp move) consists in addition/deletion of a small loop;

$\Omega _2$ (self-tangency move) is passing through a non-generic curve with a point self-tangency;

$\Omega _3$ (triple point move) is passing through a non-generic curve that has a triple point.

Figure 2: Reidemeister moves for curves
\begin{figure}\begin{center} \epsfxsize 12cm \epsfbox{moves.eps}\end{center}\end{figure}

It is evident that every curve can be untangled (taken into the standard circle) by a sequence of $\Omega _1$, $\Omega _2$, $\Omega _3$ moves (and smooth isotopies of the plane that do not influence singular points).

Conjecture. Every plane curve can be untangled using only $\Omega _1$ and $\Omega _3$ moves.

Figure 3: Untangling without $\Omega _2$ moves (place of move shown with an asterisk)
\begin{figure}\begin{center} \epsfxsize 15cm \epsfbox{untang5_1.eps}\end{center}\end{figure}


Problem 4. (S. Tabachnikov) Closed curve in a foliated domain.


Consider a topologically trivial domain $D$ in the plane foliated by straightline segments. Let $C$ be a closed immersed curve in $D$. Conjecture: there are two points of $C$ on the same leaf with parallel tangent lines.

Figure 4: Parallel tangents at two points on one leaf
\begin{figure}\begin{center} \epsfxsize 8cm \epsfbox{partang.eps}\end{center}\end{figure}

This conjecture is proved in some particular cases: (1) when the lines are all parallel or pass through one point, (2) when the winding number of $C$ is non-zero. Is it true in general?


Problem 5. (V. I. Arnold, A. Ortiz) Betti numbers of parabolic sets.


Let $f(x,y)$ be a real polynomial in two variables. Denote by $P(f)$ the set of parabolic points on the surface $\{z=f(x,y)\}$, i.e. the zero set of the Hessian $H[f]=f_{xx}f_{yy}-f_{xy}^2$. Determine the maximal number of compact connected components of the set $P(f)$ for all polynomials $f$ of given degree $n$.

This problem can be viewed as a specialization of the classical oval counting problem for polynomials representable in the form of a Hessian.

The first case when the answer is unknown is $n=4$. Then $m=\deg H[f]=\deg f =4$, and the Harnack inequality ensures that $b_0(P(f)) \le (m-1)(m-2)/2+1 =4$. There is a well-known construction of a polynomial ( $uv-\varepsilon $, where $u=0$, $v=0$ are equations of ellipses that intersect in 4 points and $\varepsilon $ is a small number) for which this estimate is attained. It is not known if it can be attained for polynomials of the form $H[f]$.


Problem 6. (V. I. Arnold) Caustics of periodic functions.


Let $g:S^1\to\mathbb{R}$ be a smooth function and $u$, $v$ two real parameters. The plane curve

\begin{displaymath} C_g = \{(u,v)\mid\mbox{ function } G_{u,v}(\varphi )=g(\varphi )+a\cos\varphi + b\sin\varphi \mbox{ is not Morse}\} \end{displaymath}

is called the caustic of the function $g$. The condition that $G_{u,v}(\varphi )$ is not Morse means that there exists a value $\varphi \in S^1$ such that $G'_{u,v}(\varphi )=G''_{u,v}(\varphi )=0$ (derivatives over $\varphi $).

Example. The caustic of the function $g(\varphi )=\cos2\varphi $ is the astroid $u=-4\cos^3\varphi $, $v=4\sin^3\varphi $.

For generic (Morse) functions $g$ caustics are fronts (smooth curves with generic singularities) that satisfy a number of specific conditions:

1. A caustic has at least 4 cusps.

2. The number of cusps is even.

3. If $P_1$, $P_2$, ..., $P_{2n}$ are cusps, then the barycentres of the sets $P_1$, $P_3$, ..., $P_{2n-1}$ and $P_2$, $P_4$, ..., $P_{2n}$ coincide. In particular, if $n=2$, they form a parallelogram.

4. The alternating length of a caustic (we change sign after each cusp) is 0.

5. From every point of the plane one can draw at least two tangents to the caustic.

6. Caustics do not have inflexion points.


Problem. Describe all curves that are caustics of periodic functions, i.e. give a necessary and sufficient condition for a front to be a caustic.


Problem 7. (V. Vassiliev) Loops in the space of knots.


Given the figure-eight knot (or any other non-trivial knot equivalent to its mirror image), let us join it with its mirror image by a path in the space of knots, and then consider the mirror image of this path.

Figure 5: Deformation of figure 8 knot into its mirros image
\begin{figure}\begin{center} \epsfxsize 16cm \epsfbox{deform8.eps}\end{center}\end{figure}

What can be said on the homology (or homotopy) class of the obtained closed loop in the space of knots? Is it trivial?


Problem 8. (A. Skopenkov) Plane projection of a spacial line arrangement.


A number of lines is drawn in the plane so that each line is parallel either to the $x$-axis or to the $y$-axis. The intersection points of these lines are marked so as to show which lines should go above the other. When such a picture can be realized as a projection of a set of lines in 3-space? Does the answer depend only on combinatorial picture or also on geometry (i.e. on distances between intersection points)?

Figure 6: A configuration not realizable by straight lines
\begin{figure}\begin{center} \epsfxsize 5cm \epsfbox{6lines.eps}\end{center}\end{figure}


Problem 9. (D. von der Flaass) Real sequence under constraints.


A doubly-infinite sequence $\{x_n\}_{n\in\mathbb{Z}}$ is said to satisfy the constraints function $f(d)$ defined for all positive integers $d$ if $\vert x_n-x_m\vert\geq f(\vert n-m\vert)$ for all $n\neq m$. For the constraints function $f(d)=1/d$, find the minimum span of a sequence satisfying it. By the span (finite or infinite) we mean the difference of the supremum and the infimum of the sequence. The conjectured answer is $\varphi +1$, where $\varphi =(1+\sqrt{5})/2$, is the golden ratio. This span is achieved by the sequence $x_n=n\mbox{ mod }(\varphi +1)$. For a motivation and some details, see http://www.cdam.lse.ac.uk/Reports/Abstracts/cdam-98-12.html


Problem 10. (S. Duzhin) Decomposable skew functions.


A (real) function of $n$ (real) variables is said to be skew-symmetric, if it changes sign whenever any two variables are interchanged:

\begin{displaymath} f(x_1,...,x_i,...,x_j,...,x_n) = -f(x_1,...,x_j,...,x_i,...x_n). \end{displaymath}

A skew-symmetric function $f(x_1,...,x_n)$ is decomposable, if there exist functions of one variable $f_1$, ..., $f_n$ such that

\begin{displaymath} f(x_1,...,x_n) = \det\Vert f_i(x_j)\Vert_{i,j=1}^n. \end{displaymath}


Theorem. In the class of analytic functions (or in any ring of functions without zero divisors) a skew-symmetric function $f(x_1,...,x_n)$ is decomposable if and only if it satisfies the identity

\begin{displaymath} f(x_1,x_2,...)f(x_3,x_4,...) - f(x_1,x_3,...)f(x_2,x_4,...) + f(x_1,x_4,...)f(x_2,x_3,...) = 0, \end{displaymath} (1)

where the dots mean one and the same set of $(n-2)$ variables.


Now, besides the above notion of complete decomposability, one can consider partially decomposable skew-symmetric functions. If $\lambda=(\lambda_1,...,\lambda_k)$ is a partition of $n$, then by a $\lambda$-decomposable skew-symmetric function of $n$ variables we understand the complete antisymmetrization of the product of $k$ arbitrary functions of $\lambda_1$, ..., $\lambda_k$ variables. The partition $(1,1,...,1)$ gives completely decomposable functions, while the partition $(n)$ yields the class of all skew-symmetric functions in $n$ variables.


Problem. For a given $\lambda\vdash n$, find a criterion of $\lambda$-decomposability.


Problem 11. (S. Duzhin) Hilbert's Sixteenth problem with separated variables.


Hilbert's sixteenth problem concerns the number and mutual position of ovals (circular connected components) of an algebraic curve defined by the equation $\varphi (x,y)=0$. We ask the same questions in the case of polynomials with additively separated variables: $\varphi (x,y)=f(x)-g(y)$ and, in particular, $\varphi (x,y)=f(x)-f(y)$. If the polynomial $f(x)$ is a Morse function ($f'(x)$ has no multiple roots), then the curve $\varphi (x,y)=0$ consists of one infinite straightline component $x=y$ and a number of ovals. The combinatorics of the oval arrangement depends only on the up-down permutation that describes the order of critical values of the polynomial.

Figure 7: Graph of $f(x)$ and the curve $f(x)=f(y)$
\begin{figure}\begin{center} \epsfxsize 12cm \epsfbox{f(x)=f(y).eps}\end{center}\end{figure}


Problem 12. (W. Known) Big Moore Graph.


The Big Moore Graph is defined as a regular graph of degree 57 with 3250 vertices and diameter 2. Problem: does it exist? In other words, is it possible to organize air traffic in a country with 3250 cities so that there are 57 air routes flying from each city and any two cities are connected either by a direct flight or by two consecutive flights with one transfer?

These problems were announced on October 5, 2001 at the Moscow-Petersburg seminar on Low-Dimensional Mathematics.
Names in parenthesis refer to authors or people who communicated to me these problems. Some problems come with additions and modifications on my part.
Home page of the seminar http://www.pdmi.ras.ru/~lowdimma

Sergei Duzhin 2001-10-13