"Combinatorial PL-fiber-bundles and fragmentation of
fiberwise homeomorphism" Preprint PDMI 12-06
Russian. pdf
109 pp. 700 KB version 30.04.07. Published in Zapiski
Nauchnyh Seminarov POMI ,v344, p 56-173, 2007. English
translation is located in ArXiv arXiv:0708.4039 and published in Journal of Mathematical Sciences
Vol 145 No 3, 2007.
===========
==============
Abstract
With a compact PL manifold X we associate a category T(X). The objects
of
T(X) are all combinatorial manifolds of type X, and morphisms are
combinatorial
assemblies. We prove that the homotopy equivalence BT (X) \approx
BPL(X) holds,
where PL(X) is the simplicial group of PL-homeomorphisms. Thus the
space BT(X)
is a canonical countable (as a CW-complex) model of BPL(X). As a
result, we
obtain functorial pure combinatorial models for PL fiber bundles with
fiber X
and a PL polyhedron B as the base. Such a model looks like a
T(X)-coloring of
some triangulation K of B. The vertices of K are colored by objects of
T(X) and
the arcs are colored by morphisms in such a way that the diagram
arising from
the 2-skeleton of K is commutative. Comparing with the classical
results of
geometric topology, we obtain combinatorial models of the real
Grassmannian in
small dimensions: BT(S^{n-1}) \approx BO(n) for n=1,2,3,4. The result
is proved
in a sequence of results on similar models of B\PL(X). Special
attention is
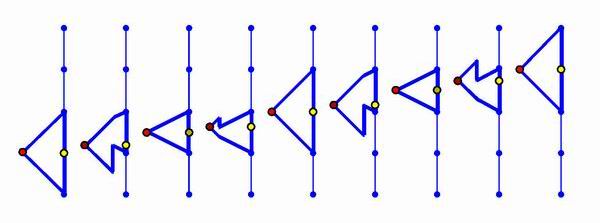
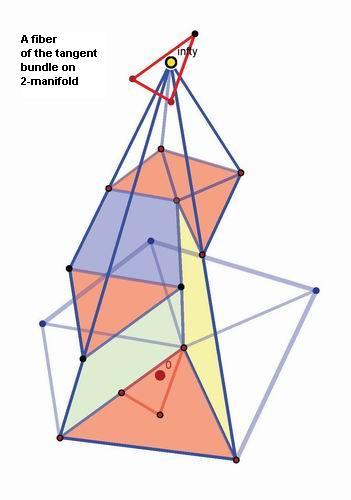
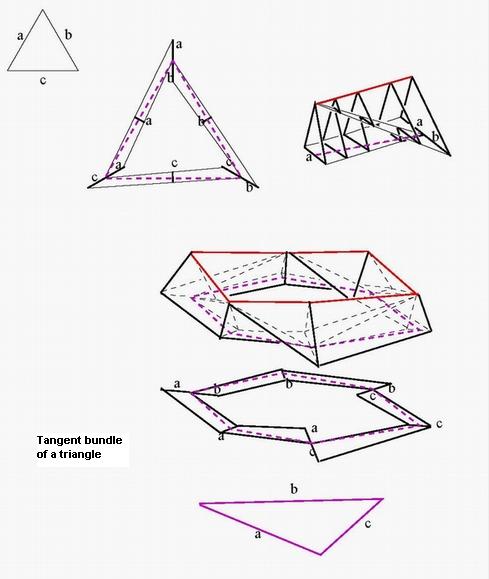
paid to the main noncompact case X=R^n and to the tangent bundle and
Gauss
functor of a combinatorial manifold. The trick that makes the proof
possible is
a collection of lemmas on "fragmentation of a fiberwise homeomorphism",
a
generalization of the folklore lemma on fragmentation of an isotopy.
========================
The note
"
Tangent
bundle and Gauss functorof
a combinatorial manifold"
math.GT/0609257
contains a brief English extract from the manuscript.
Here is the slides from the talk "Combinatorial Fiber Bundles" at Admont (Austria), July 2009