Outline of results
Patchworking: constructing real algebraic varieties with
controlled topological properties
Although I started in low-dimensional topology, I seem to be best known
my contributions to real algebraic geometry.
As far as I can judge, my most appreciated invention is the patchwork
technique or ``Viro method'' which allows real algebraic varieties to be
constructed by a sort of ``cut and paste'' technique. It was introduced
in order to construct real algebraic varieties
with remarkable topological properties. Using it I have completed the
classification up to isotopy of non-singular plane projective curves
of degree 7 and disproved the classical Ragsdale conjecture formulated
in 1906 [13]. See also [16], [17], [18], [20],
[23], [34], [42] and [55].
The dequantizing of algebraic geometry; tropical
geometry
In my talk [47] at the third European Congress of Mathematicians
in 2000, I observed
that real algebraic geometry can be presented as a quantized
(i.e., deformed) piecewise linear geometry. A simple version of the
patchwork construction (which builds a real algebraic hypersurface in
a toric variety out of a special piecewise-linear hypersurface of
Euclidean space) could be understood in terms of this quantization.
The generalization of these ideas gave rise to the development (by Kapranov,
Kontsevich, Sturmfiels and Mikhalkin) of so called tropical geometry
and its applications to problems of classical algebraic geometry.
Other results on real algebraic varieties
I found several restrictions on the topology of real algebraic curves (see
[10], [17], [18], [27], [38]),
explicit elementary constructions of real algebraic surfaces with
maximal total Betti numbers [11], and non-singular real projective
quartic
surfaces of all but one of the possible isotopy types [12].
I generalized complex
orientations from the simple case of a real algebraic curve dividing
its complexification
to real algebraic varieties of high dimensions [15], [39].
Together with Kharlamov I generalized the main topological
restrictions on nonsingular plane projective real algebraic curves
to singular ones [27]. Recently, in a joint paper [48]
with Orevkov, I managed,
by applying one of these results on singular curves, to prove
Orevkov's conjecture on the topology of nonsingular curves of degree 9.
I studied the Radon transformations based on integrals against the Euler
characteristic on real and complex
projective spaces, and established its relation to the projective
duality for algebraic varieties [26]. This gives new
relations between the numerical characteristics of projectively dual
varieties.
TQFT
Jointly with V. Turaev, I found a (2+1)-dimensional topological
quantum field theory based on state sums over triangulations or Heegaard
diagrams and involving quantum 6j-symbols, see [35].
This paper had unexpected (to the authors) relations to Physics: it
gave the first rigorous realization of the approach by G. Ponzano and
T. Redge to 2+1 quantum gravity. In the context of Quantum Topology,
it was widely generalized and related to other quantum invariants.
From the algebraic point of view, the invariants introduced in [35]
are based on the representation theory of quantum group 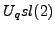 where
the parameter
where
the parameter 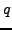 is a root of unity. In [51] I used similar
constructions applied to the quantum super-group
is a root of unity. In [51] I used similar
constructions applied to the quantum super-group
 and
and
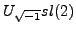 to study quantum relatives of the Alexander
polynomial.
to study quantum relatives of the Alexander
polynomial.
Exotic knottings
Jointly with S.Finashin and M.Kreck, I constructed the first infinite
series of surfaces smoothly embedded in the 4-sphere, which are pairwise
ambiently homeomorphic, but not diffeomorphic, see [24], [25].
The examples come from real algebraic geometry. Namely, the series
of Dolgachev surfaces has real structures (that is complex conjugation
involutions) the orbit spaces spaces of which are diffeomorphic to the
4-sphere. The real point sets (i.e., the fixed point sets of the
involutions) are diffeomorphic to the connected sum of 5 copies of the
Klein bottle. They are embedded in the 4-sphere differently from the
differential viewpoint, because the Dolgachev surfaces are not
diffeomorphic, but in the same way topologically. (In the paper only
finiteness of topological types was proven, but later Kreck proved
that there is only one type.)
Diagrammatic formulas for finite type invariants
In a joint work [40] with M.Polyak, I introduced diagrammatic formulas
for Vassiliev knot invariants. Joint work [44] with
M. Goussarov and M. Polyak extended these formulas and the notion of
Vassiliev invariants to virtual knots.
For the Arnold invariants of generic immersed plane curves, I found
counter-parts for real plane algebraic curves. This, together with
Rokhlin's complex orientations formula for real algebraic curves
suggested combinatorial formulas for the Arnold invariants 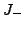 and
and 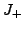 .
The formulas allowed me to prove Arnold's conjecture about the
range of these invariants. See [41].
.
The formulas allowed me to prove Arnold's conjecture about the
range of these invariants. See [41].
Real algebraic links
I initiated the topological study of generic configurations of lines
in 3-space. See [22], [31] and [32]. For non-singular real
algebraic curves in
3-dimensional projective space, I defined a numerical characteristic
(the ``encomplexed'' writhe number) invariant under rigid isotopy, which
allows the proof that some real algebraic curves, which are
topologically isotopic, cannot be deformed to each other in the
class of non-singular real algebraic curves. See [46].
Curves generically immersed in the plane can be considered as the counter-part
of links in 3-space, since their natural liftings to the unit
tangent bundle and to the
projectivized tangent bundle are knots in these 3-manifolds. Arnold's
invariants 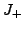 and
and 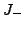 are isotopy invariants of the corresponding knots.
An even more profound invariant is the Whitney number classifying
immersions of the circle into the plane up to regular homotopy.
In [53] I
found an expression for the Whitney number of a closed real algebraic
plane affine curve dividing its complexification and equipped with a
complex orientation, in terms of the behavior of its complexification
at infinity.
are isotopy invariants of the corresponding knots.
An even more profound invariant is the Whitney number classifying
immersions of the circle into the plane up to regular homotopy.
In [53] I
found an expression for the Whitney number of a closed real algebraic
plane affine curve dividing its complexification and equipped with a
complex orientation, in terms of the behavior of its complexification
at infinity.
Branched coverings
During my study at Leningrad State University, I proved that any
closed orientable 3-manifold of genus two is a two-fold branched
covering of the
3-sphere branched over a link with 3-bridges [1], [3] (this
was proven independently by
Joan S.Birman and H.Hilden); I also found interpretations of the signature
invariants of a link of codimension 2 as signature invariants of cyclic
branched covering spaces of a ball, and proved estimates for the slice genus
of links and the genus of non locally flat surfaces in 4-manifolds [4],
[6].
Research plans
By a research plan one often means either an account of research
which has been done, but is yet not documented in papers or
preprints, or a statement of research intentions. It provides a sort
of research self-portrait of the author,
especially valuable at the beginning of his/her career, right after the
Ph.D, when a statement on completed research looks short.
After 37 years of research in Mathematics an
outline of main results says more. In fact, my research plans were
never on a par with results. I was never able to foresee really
interesting discoveries and new twists of the subject, which ended up
drastically changing the direction of my research.
After this disclaimer, let me restrict myself to an indication of wide
directions, in which I plan to concentrate. I do have more detailed
plans, but my experience suggests that the details most probably
will change.
Categorification of combinatorial invariants
In low dimensional topology, there is a long standing challenge
to bridge the combinatorial topology of knots and 3-manifolds with the
gauge-theoretic topology of 4-manifolds.
Two major breakthroughs in low dimensional topology, that happened in
the eighties, were motivated by ideas which came from physics. First,
S. Donaldson discovered new invariants of differential 4-dimensional
manifolds by studying solutions of the Yang-Mills equation. Second, a
new class of combinatorial invariants of knots and 3-dimensional
manifolds was discovered. This class includes the Jones polynomial and
Reshetikhin - Turaev invariant of 3-manifolds and is related to quantum
groups.
The topological invariants which emerged in these two revolutions
appeared to be quite different. The Donaldson invariants and, closely
related to them, the Seiberg-Witten invariants of 4-manifolds are based on
heavy analytical techniques from partial differential equations. They led
to the discovery of a great variety of smooth structures on 4-manifolds, a
phenomenon which distinguishes dimension 4 from all the other
dimensions. The analytic nature of these invariants challenges topologists:
general, well-known results imply that all the invariants of smooth
structures on 4-manifolds should have combinatorial definitions, which
are standard for topology. A combinatorial definition would be very
useful both for the calculation of the invariants, and for the
understanding of their nature.
The quantum invariants of links and 3-manifolds were understood
combinatorially from the very beginning. Immediately after their
introduction, M. F. Atiyah conjectured that they are related to the
Donaldson invariants. This would give a combinatorial perspective on the
Donaldson invariants. Although the relation has not yet been found,
there has been a real progress in this direction.
In a recent work by M. Khovanov on categorification of the
Jones polynomial, the Kauffman state sum construction for the Jones
polynomial of a link was elevated to a construction of a bigraded
family of homology groups related to the Jones polynomial in the same
way as the usual homology groups of a topological space are related to its
Euler characteristic. This provided a new approach to the problem
under consideration.
Then Ozsvath and Szabo constructed a version of Floer homology theory
and, using it, made a categorification of the Alexander-Conway polynomial.
Their construction was not entirely combinatorial, but in 2006
Manolescu, Ozsvath and Sarkar proposed a purely combinatorial construction.
This categorification looks very similar to Khovanov
homology. These two homology theories share so many properties that
one could even suspect the existence of a homology theory, which would
generalize both of them, as the HOMFLY polynomial generalizes both
underlying polynomials, the Alexander and the Jones polynomials.
Indeed, in a recent
preprints by Khovanov and Rozansky, the HOMFLY polynomial was
categorified, and
conjecturally both the Khovanov homology and the Ozsvath-Szabo Heegaard Floer
homology can be recovered from this categorification.
Besides the conceptual simplification and clarification of the
subject, one may expect that the new homology theories will bring new
results and new simpler proofs of known geometric results.
To some extent,
these hopes have started to come true: recently Rasmussen, Livingston and
Shumakovitch managed to find new proofs, based on these new homology
theories, for the most exciting results obtained originally via gauge theory
on the slice genus of knots.
There are many open problems in this direction. First of all, the major
problem is to extend the combinatorial categorifications of quantum
polynomials to invariants of 3- and 4-manifolds. Second,
categorifications of quantum polynomial link
invariants should be generalized to links in an arbitrary 3-manifold.
During the last few years I have worked in this direction. So far only partial results
have been obtained. Khovanov homology has been generalized to virtual links,
and links in thickened surfaces. At the first stage, unexpectedly, a
full-fledged categorification with integer coefficients required an
additional assumption on the virtual links. As a by-product, I constructed
Khovanov homology for links in projective space. In May 2006
V. O. Manturov managed to eliminate these additional assumptions on
virtual links. This opens a new perspective for work in this direction.
I mean to continue this research.
The state sum models that I studied in [51] provide opportunities
for combinatorial categorification of invariants related to the
Alexander polynomial. This is a promising, although technically
involved,
problem that I am working on now.
Real algebraic knot theories
In classical knot theory by a link one means a smooth closed
1-dimensional submanifold of the 3-dimensional sphere 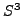 ,
i. e. several disjoint circles smoothly embedded in
,
i. e. several disjoint circles smoothly embedded in 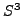 .
.
A classical link may emerge as
the set of real points of a real algebraic curve. First, this gives rise
to questions about relations between the invariants of the same curve
provided by link theory and by algebraic geometry.
Second, this suggests to develop a theory
parallel to the classical link theory, but taking into account the
algebraic nature of the objects. From this viewpoint it is more
natural to consider real algebraic links up to an isotopy consisting of
real algebraic links belonging to the same continuous family of
algebraic curves, rather than up to smooth isotopy in the class of
classical links. An isotopy of the former kind is called a rigid
isotopy.
Of course, there is a forgetful functor: any real algebraic link
can be considered as a classical link and a rigid isotopy as a smooth
isotopy. It is interesting, how much is lost in this transition.
There is another forgetful functor: a real algebraic link can be
considered over the field of complex numbers. A rigid isotopy gives rise
to a path in the moduli space of the corresponding non-singular complex
algebraic curves embedded into the complexification of the ambient
3-manifold. These moduli spaces are known to be numerous and complicated.
A path-connected component of moduli space containing the
complexification of a real algebraic link is invariant under rigid
isotopy of that link. Thus instead of a single real algebraic knot
theory we see a special real algebraic link theory for each
path-connected component of moduli space. The most elementary of those
components consist of rational curves.
The tools coming from the classical knot theory did not apply easily and
naturally to real algebraic knots. However finite type invariants
and especially their recent geometric interpretations seem to fit
better.
Tropical geometry
This is a geometry based on the group of real affine transformations
with linear part belonging to
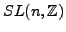 . It can be viewed also
as an algebraic geometry over the semi-field of real numbers with
operations of taking maximum (for addition) and addition (for
multiplication). It is closely related
to algebraic geometry over the complex or real numbers and, especially,
over the fields of Puiseux series. Although tropical varieties have appeared
in many situations and proved to be useful, the main notions related to
them are still to be developed. The combinatorial patchworking that I
discovered about 25 years ago is now considered as real tropical
hypersurfaces. Other classes of tropical varieties, for instance curves in
3-space, are yet to be studied.
. It can be viewed also
as an algebraic geometry over the semi-field of real numbers with
operations of taking maximum (for addition) and addition (for
multiplication). It is closely related
to algebraic geometry over the complex or real numbers and, especially,
over the fields of Puiseux series. Although tropical varieties have appeared
in many situations and proved to be useful, the main notions related to
them are still to be developed. The combinatorial patchworking that I
discovered about 25 years ago is now considered as real tropical
hypersurfaces. Other classes of tropical varieties, for instance curves in
3-space, are yet to be studied.
Differential spaces
I plan to revise the foundations of differential topology and geometry.
The goal is to make them more similar to the foundations of algebraic
geometry. Their present state does not allow discussion of manifolds with
singularities, quotient spaces, etc. I believe that a more flexible system
of notions is needed in research, teaching, and applications.
In the sixties a few attempts were made to introduce the category of
differential
spaces, but they failed to be accepted by the mainstream
research community. I believe this will require additional research,
and I plan to take a look in this direction.
-
- 1
- Links, two-fold branched coverings and braids, Matem.
sbornik 87:2 (1972) 216 - 228 (Russian); English translation
in Soviet Math. Sbornik.
- 2
- Local knotting of submanifolds, Matem. sbornik 90:2
(1973) 172-181 (Russian);
English translation in Soviet Math. Sbornik.
- 3
- Two-fold branched coverings of three-dimensional sphere, Zap.
Nauchn. Semin. LOMI 36 (1973) 6-39 (Russian); English transl.
in J. Soviet Math 8:5 (1977) 531-553.
- 4
- Branched coverings of manifolds with boundary and invariants of links.
I, Izvestiya AN SSSR, ser. Matem. 37:6 (1973) 1242-1259
(Russian); English translation in Soviet Math. Izvestia.
- 5
- Non-projecting isotopies and knots with homeomorphic covering spaces,
Zap. Nauchn. Semin. LOMI 66 (1976) Russian;
English transl. in J. Soviet Math. 12:1
(1979) 86-96.
- 6
- Placements in codimension 2 and boundary, Uspekhi Mat. Nauk
30:1 (1975) 231-232 (Russian).
- 7
- The Volodin-Kuznetsov-Fomenko conjecture on Heegaard diagrams of
3-dimensional sphere is not true, (joint with V. L. Kobelsky),
Uspekhi Mat. Nauk 32:5 (1977) 175-176 (Russian).
- 8
- Signatures of links, Tezisy VII Vsesoyuznoj topologicheskoj konferencii
(1977) 41 (Russian).
- 9
- Estimates for twisted homology,(joint with V. G. Turaev), Tezisy VII
Vsesoyuznoj topologicheskoj konferencii (1977) 42 (Russian).
- 10
- Generalizing Petrovsky and Arnold inequalities for curves with
singularities, Uspekhi Mat. Nauk 33:3 (1978) 145-146 (Russian).
- 11
- Constructing M-surfaces, Funkts. analiz i ego prilozh. 13:3 (1979) 71-72 (Russian); English transl. in Functional Anal.
Appl. 13:3 (1979).
- 12
- Constructing multicomponent real algebraic surfaces, Doklady
AN SSSR 248:2 (1979) 279-282 (Russian); English transl. in
Soviet Math. Doklady.
- 13
- Curves of degree 7, curves of degree 8 and Ragsdale conjecture,
Doklady AN SSSR 254:6 (1980) 1305-1310 (Russian);
English transl. in Soviet Math. Doklady.
- 14
- Colored knots, Kvant (1981) No. 3, 8-14 (Russian);
English translation: Tied into Knot Theory: unraveling the basics
of mathematical knots. Quantum 8 (1998), no. 5, 16-20.
- 15
- Complex orientations of real algebraic surfaces, Uspekhi Mat.
Nauk 37:4 (1982) 93 (Russian).
- 16
- Gluing algebraic hypersurfaces and constructions of curves, Tezisy
Leningradskoj Mezhdunarodnoj Topologicheskoj Konferencii 1982,
Nauka (1983) 149-197 (Russian).
- 17
- Plane real algebraic curves of degrees 7 and 8: new restrictions,
Izvestiya AN SSSR, ser. Matem. 47:5 (1983) 1135-1150 (Russian);
English transl. in Soviet Math. Izvestia.
- 18
- Progress over the last 5 years in topology of real algebraic
varieties, Proceedings of the International Congress of Mathematicians,
Aug. 16 - 24, 1983 vol. 1, Warszawa PWN, Warsaw 595-611 (Russian).
- 19
- Intersections of loops on two-dimensional manifolds. II. Free loops
(joint with V. G. Turaev), Mat. sbornik 121:3 (1983) 359-369
(Russian); English translation in Soviet Math. Sbornik.
- 20
- Gluing of plane real algebraic curves and constructions of curves of
degrees 6 and 7, Lecture Notes in Math. 1060 (1984) 187-200,
Springer-Verlag, Berlin and New York.
- 21
- The signature of a branched covering, Mat. zametki 36:4
(1984) 549-557 (Russian); English translation in Math. Notes
36:3 4772-776.
- 22
- Topological problems on lines and points of the three-dimensional
space, Doklady AN SSSR 284:5 (1985) 1049-1052 (Russian);
English translation in Soviet Math. Doklady 32:2 (1985) 528-531
.
- 23
- Progress of the last six years in topology of real algebraic
varieties, Uspekhi Mat. Nauk 41:3 (1986) 45-67 (Russian)
English translation in Russian Math. Surveys 41:3 (1986) 55-82.
- 24
- Exotic knottings of surfaces in the 4-sphere (joint with S. M. Finashin and
M. Kreck), Bull. Amer. Math. Soc. 17:2 (1987) 287-290.
- 25
- Non-diffeomorphic but homeomorphic knottings of surfaces in the 4-sphere
(joint with S. M. Finashin and M. Kreck), Lecture Notes in Math.
1346 (1988) 157-198, Springer-Verlag, Heidelberg and New-York.
- 26
- Some integral calculus based on Euler characteristic,
Lecture Notes in Math.
1346 (1988) 127-138, Springer-Verlag, Heidelberg and New-York.
- 27
- Extensions of the Gudkov-Rohlin congruence (joint with V.M.Kharlamov)
Lecture Notes in Math. 1346 (1988) 357-406, Springer-Verlag,
Heidelberg and New-York.
- 28
- Introduction to homotopy theory (joint with D.B.Fuchs),
Current problems in mathematics. Fundamental
directions, Vol. 24, 6-121, Itogi Nauki i Tekhniki,
Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow,
1988 (Russian). English translation by C. J. Shaddock, Encyclopaedia Math. Sci., 24, Topology. II, 1-93, Springer, Berlin, 2004.
- 29
- Homology and cohomology (joint with
D.B.Fuchs), Current problems in mathematics. Fundamental directions,
Vol. 24, 123-240, Itogi Nauki i Tekhniki, Akad. Nauk SSSR,
Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1988 (Russian).
English translation
by C. J. Shaddock, Encyclopaedia Math. Sci., 24, Topology. II, 95-196,
Springer, Berlin, 2004.
- 30
- Problems in Topology (joint with O. A. Ivanov, N. Yu. Netsvetaev
and V. M. Kharlamov), Leningrad, LGU, 1988 (Russian);
Second, extended edition: St. Petersburg, SPbU, 2000.
- 31
- Interlacing of skew lines (joint with J.V.Drobotukhina) Kvant (1988)
No. 3, 12-19 (Russian).
- 32
- Configurations of skew lines (joint with Ju.V.Drobotukhina),
Algebra i analiz 1:4 (1989) 222-246 (Russian)
English translation in
Leningrad Math. J. 1:4 (1990) 1027-1050.
- 33
- Compact four-dimensional exotica with small homology,
Algebra i analiz 1:4 (1989) 67-77 (Russian);
English translation in Leningrad Math. J. 1:4 (1990)
871-880.
- 34
- Plane real algebraic curves: constructions with controlled topology
Algebra i analiz 1:5 (1989) 1-73 (Russian);
English translation in Leningrad Math. J. 1:5 (1990) 1059-1134.
- 35
- State sum invariants of 3-manifolds and quantum 6j-symbols (joint with
V. G. Turaev), Topology 31:4 (1992) 865-902.
- 36
- Lectures on combinatorial presentations of manifolds, In book
Differential geometry and topology (Alghero, 1992) World Sci. Publ.,
River Edge, NJ (1993) 244-264.
- 37
- Moves of triangulations of a PL-manifold. Quantum groups
(Leningrad, 1990), 367-372, Lecture Notes in Math., 1510,
Springer, Berlin, 1992.
- 38
- An inequality for the number of nonempty ovals of a curve of odd degree
(joint with V. I. Zvonilov), Algebra i analiz 4:3 (1992) 159-170
(Russian); English translation in St. Petersburg Math. J. 4:3 (1993).
- 39
- Complex orientations of real algebraic surfaces, Topology of manifolds and
varieties, Advances of Soviet Math. 18 (1994), 261-284; see also
arXive: math.AG/0611396.
- 40
- Gauss diagram formulas for Vassiliev invariants,(joint with Michael Polyak)
International Mathematics Research Notes 1994:11.
- 41
- Generic immersions of circle to surfaces and complex topology
of real algebraic curves, Topology of real algebraic varieties and relate
d topics, (
a volume dedicated to memory of D. A. Gudkov ), AMS Translations,
Series 2, 173, (1995) 231-252 .
- 42
- Patchworking algebraic curves disproves the Ragsdale
conjecture, (joint with Ilia Itenberg), The Mathematical
Intelligencer 18:1 (1996), 19-28.
- 43
- Mutual position of hypersurfaces in projective
space. Geometry of differential equations, 161-176, Amer. Math.
Soc. Transl. Ser. 2, 186, Amer. Math. Soc., Providence, RI,
1998.
- 44
- Finite type invariants of classical and virtual knots,
(joint with M. Goussarov and M. Polyak), Topology 39:5,
(2000) 1045-1068; see also arXiv: math. GT/9810073.
- 45
- On the Casson knot invariant, (joint with Michael Polyak),
J. Knot Theory and Its Ramifications 10:5 (2001) 711-738; see also arXiv:math.GT/9903158.
- 46
- Encomplexing the writhe. Topology, ergodic
theory, real algebraic geometry, 241-256, Amer. Math. Soc. Transl.
Ser. 2, 202, Amer. Math. Soc., Providence, RI, 2001; see also
arXiv: math.AG/0005162.
- 47
- Dequantization of Real Algebraic Geometry on a
Logarithmic Paper, Proceedings of the 3rd European Congress of
Mathematicians, Birkhäuser,
Progress in Math, 201, (2001),
135-146; see also arXiv: math.AG/0005163.
- 48
- Congruence modulo 8 for real algebraic curves of degree 9.
(joint with S. Yu. Orevkov)
Uspekhi Mat. Nauk 56 (2001), no. 4(340), 137-138 (Russian);
English translation in Russian Math. Surveys 56 (2001),
no. 4, 770-771.
- 49
- What is an amoeba, Notices AMS, 49:8 (2002), 916-917.
- 50
- Remarks on definition of Khovanov homology, arXiv:math.GT/0202199
(2002).
- 51
- Quantum relatives of Alexander polynomial, arXiv:math.GT/0204290
(2002), St.Petersburg Mathematical Journal, 18:3 (2006)
63-157 (Russian), to be published in English in
St.Petersburg Math. J.
- 52
- Khovanov homology, its definitions and ramifications, Fund.
Math. 184 (2004), 317-342.
math.GT/0204290
- 53
- Whitney Number of Closed Real Algebraic Affine Curve of Type I,
Moscow Mathematical Journal 6:1 (2006); see also arXiv:
math.AG/0602256.
- 54
- Virtual Links, Orientations of Chord Diagrams and Khovanov Homology,
Proceedings of 12th Gökova Geometry-Topology Conference 2005, International
Press, 2006, 187-212; see also arXiv: math.GT/0611406.
- 55
- Asymptotically Maximal Real Algebraic Hypersurfaces of Projective Space, (joint with Ilia Itenberg) Proceedings of 13th Gökova Geometry-Topology Conference
2006, International Press, 2007, accepted for publication.
Oleg Viro
2007-11-25
![]() where
the parameter
where
the parameter ![]() is a root of unity. In [51] I used similar
constructions applied to the quantum super-group
is a root of unity. In [51] I used similar
constructions applied to the quantum super-group
![]() and
and
![]() to study quantum relatives of the Alexander
polynomial.
to study quantum relatives of the Alexander
polynomial.
![]() and
and ![]() .
The formulas allowed me to prove Arnold's conjecture about the
range of these invariants. See [41].
.
The formulas allowed me to prove Arnold's conjecture about the
range of these invariants. See [41].
![]() and
and ![]() are isotopy invariants of the corresponding knots.
An even more profound invariant is the Whitney number classifying
immersions of the circle into the plane up to regular homotopy.
In [53] I
found an expression for the Whitney number of a closed real algebraic
plane affine curve dividing its complexification and equipped with a
complex orientation, in terms of the behavior of its complexification
at infinity.
are isotopy invariants of the corresponding knots.
An even more profound invariant is the Whitney number classifying
immersions of the circle into the plane up to regular homotopy.
In [53] I
found an expression for the Whitney number of a closed real algebraic
plane affine curve dividing its complexification and equipped with a
complex orientation, in terms of the behavior of its complexification
at infinity.
![]() ,
i. e. several disjoint circles smoothly embedded in
,
i. e. several disjoint circles smoothly embedded in ![]() .
.
![]() . It can be viewed also
as an algebraic geometry over the semi-field of real numbers with
operations of taking maximum (for addition) and addition (for
multiplication). It is closely related
to algebraic geometry over the complex or real numbers and, especially,
over the fields of Puiseux series. Although tropical varieties have appeared
in many situations and proved to be useful, the main notions related to
them are still to be developed. The combinatorial patchworking that I
discovered about 25 years ago is now considered as real tropical
hypersurfaces. Other classes of tropical varieties, for instance curves in
3-space, are yet to be studied.
. It can be viewed also
as an algebraic geometry over the semi-field of real numbers with
operations of taking maximum (for addition) and addition (for
multiplication). It is closely related
to algebraic geometry over the complex or real numbers and, especially,
over the fields of Puiseux series. Although tropical varieties have appeared
in many situations and proved to be useful, the main notions related to
them are still to be developed. The combinatorial patchworking that I
discovered about 25 years ago is now considered as real tropical
hypersurfaces. Other classes of tropical varieties, for instance curves in
3-space, are yet to be studied.