4.3 Complex Orientations and Pencils of Lines. Alternative Approach

In proofs of 3.8.G, 3.8.H and 3.8.I, the theory developed in the previous section can be replaced by the following Theorem 4.3.A. Although this theorem can be obtained as a corollary of Theorem 4.2.C, it is derived here from Theorem 2.3.A and the complex orientation formula, and in the proof no chain of ovals is used. The idea of this approach to Fiedler's alternation of orientations is due to V. A. Rokhlin.

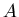
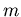
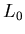
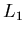
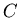
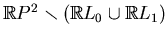
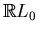
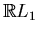
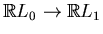
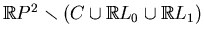
4.3.A   Let $A$ be a non-singular dividing curve of degree $m$. Let $L_0$, $L_1$ be real lines, $C$ be one of two components of $\mathbb{R}P^2\smallsetminus (\mathbb{R}L_0\cup\mathbb{R}L_1)$. Let $\mathbb{R}L_0$ and $\mathbb{R}L_1$ be oriented so that the projection $\mathbb{R}L_0\to\mathbb{R}L_1$ from a point lying in $\mathbb{R}P^2\smallsetminus (C\cup\mathbb{R}L_0\cup \mathbb{R}L_1)$ preserves the orientations. 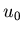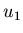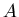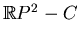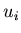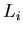Let ovals $u_0$, $u_1$ of $A$ lie in $\mathbb{R}P^2- C$ and $u_i$ is tangent to $L_i$ at one point $(i=1, 2)$. 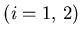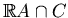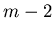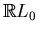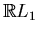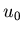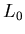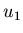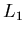If the intersection $\mathbb{R}A\cap C$ consists of $m-2$ components, each of which is an arc connecting $\mathbb{R}L_0$ with $\mathbb{R}L_1$, then points of tangency of $u_0$ with $L_0$ and $u_1$ with $L_1$ are positive with respect to one of the complex orientations of $A$.

Figure 28:

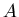
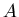
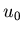
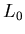
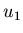
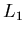
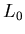
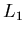
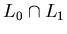
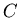
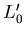
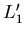
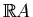
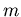
Proof. Assume the contrary: suppose that with respect to a complex orientation of $A$ the tangency of $u_0$ with $L_0$ is positive and the tangency of $u_1$ with $L_1$ is negative. Rotate $L_0$ and $L_1$ around the point $L_0\cap L_1$ in the directions out of $C$ by small angles in such a way that each of the lines $L'_0$ and $L'_1$ obtained intersects transversally $\mathbb{R}A$ in $m$ points. 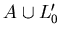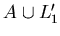Perturb the union $A\cup L'_0$ and $A\cup L'_1$ obeying the orientations. 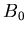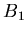By 2.3.A, the nonsingular curves $B_0$ and $B_1$ obtained are of type I. 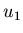It is easy to see that their complex schemes can be obtained one from another by relocating the oval, appeared from $u_1$ (see Figure 28). 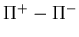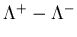This operation changes one of the numbers $\Pi^+-\Pi^-$ and $\Lambda ^+-\Lambda ^-$ by 1. Therefore the left hand side of the complex orientation formula is changed. 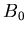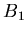It means that the complex schemes both of $B_0$ and $B_1$ can not satisfy the complex orientation formula. This proves that the assumption is not true. $\qedsymbol$