T-curves

Now let us come back to the Patchwork Theorem. It states that for any convex triangulation $\tau$ of $T$ with integer vertices and a distribution of signs at vertices of $\tau$ there exists a nonsingular real algebraic plane projective curve $A$ of degree $m$ such that the pair $(\mathbb{R}P^2,\mathbb{R}A)$ is homeomorphic to the pair $(\mathcal{T},\mathcal{L})$ constructed as in Section 1, i. e. the result of projective combinatorial patchworking.

In fact, a polynomial defining the curve can be presented quite explicitly.

Construction of Polynomials. Given initial data $m$, $T$, $\tau$ and $\sigma _{i,j}$ as in Section 1 and a convex function $\nu$ certifying that the triangulation $\tau$ is convex. Consider a one-parameter family of polynomials

$$b_t(x,y)=\sum_{\begin{aligned}&{(i,j) \text{\enspace\scriptsize r... ...d\scriptsize vertices of $\tau $}\end{aligned}}\sigma _{i,j}x^iy^jt^{\nu(i,j)}.$$

Denote by $B_t$ the corresponding homogeneous polynomials:

$$B_t(x_0,x_1,x_2)=x_0^mb_t(x_1/x_0,x_2/x_0).$$

Polynomials $b_t$ and $B_t$ are called the results of affine and projective polynomial patchworking.

2 (Detailed Patchwork Theorem)   Let $m$, $T$, $\tau$, $\sigma _{i,j}$ and $\nu$ be initial data as above. Denote by $b_t$ and $B_t$ the non-homogeneous and homogeneous polynomials obtained by the polynomial patchworking of these initial data, and by $L$ and $\mathcal{L}$ the piecewise linear curves in the square $T_*$ and its quotient space $\mathcal{T}$ respectively obtained from the same initial data by the combinatorial patchworking.

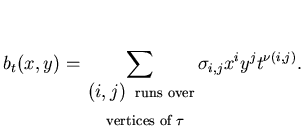
Then there exists $t_0>0$ such that for any $t\in(0,t_0]$

1. $b_t$ defines an affine curve $a_t$ such that the pair $(\mathbb{R}^2, \mathbb{R}a_t)$ is homeomorphic to the pair $(T_*, L)$;
2. $B_t$ defines a projective curve $A_t$ such that the pair $(\mathbb{R}P^2, \mathbb{R}A_t)$ is homeomorphic to the pair $(\mathcal{T},\mathcal{L})$.

A curve obtained by this construction is called a T-curve.

All real schemes of curves of degree $\le 6$ and almost all real schemes of curves of degree $7$ have been realized by the patchwork construction described above. On the other hand, there exist real schemes realizable by algebraic curves of some (high) degree, but not realizable by T-curves of the same degree. Probably such a scheme can be found even for degree $7$ or $8$.

The construction of T-curves is a special case of more general patchwork construction, see [17] and [13]. In this generalization the patches are more complicated: they may be algebraic curves of any genus with arbitrary Newton polygon. Therefore the patches demand more care than above. This is why we restrict ourselves here to T-curves. However, even constructing T-curves it is useful to think in terms of blocks more complicated than a single triangle (made of several triangles).

The rest of the paper is devoted to applications of the patchwork construction.