References beginning with O
 T. Ochiai,
The combinatorial Gauss diagram formula for Kontsevich integral,
University of Tokyo preprint, June 2000,
arXiv:math.GT/0006184.
T. Ochiai,
The combinatorial Gauss diagram formula for Kontsevich integral,
University of Tokyo preprint, June 2000,
arXiv:math.GT/0006184.
 E. Ogasa,
Ribbon-moves of 2-links preserve the
E. Ogasa,
Ribbon-moves of 2-links preserve the 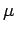 -invariant of 2-links,
University of Tokyo preprint, April 2000. See also
math.GT/0004008.
-invariant of 2-links,
University of Tokyo preprint, April 2000. See also
math.GT/0004008.
 T. Ohtsuki,
Finite type invariants of integral homology 3-spheres,
Jour. of Knot Theory and its Ramifications 5(1) (1996) 101-115.
T. Ohtsuki,
Finite type invariants of integral homology 3-spheres,
Jour. of Knot Theory and its Ramifications 5(1) (1996) 101-115.
 T. Ohtsuki,
On some invariants of 3-manifolds,
in Proc. of the Århus Conf. Geometry and physics,
(J. E. Andersen, J. Dupont, H. Pedersen, and A. Swann, eds.),
lecture notes in pure and applied mathematics 184 (1997) 411-427,
Marcel Dekker, New-York.
T. Ohtsuki,
On some invariants of 3-manifolds,
in Proc. of the Århus Conf. Geometry and physics,
(J. E. Andersen, J. Dupont, H. Pedersen, and A. Swann, eds.),
lecture notes in pure and applied mathematics 184 (1997) 411-427,
Marcel Dekker, New-York.
 T. Ohtsuki,
Combinatorial quantum method in 3-dimensional topology,
Math. Soc. of Japan Memoirs 3, Tokyo 1999.
T. Ohtsuki,
Combinatorial quantum method in 3-dimensional topology,
Math. Soc. of Japan Memoirs 3, Tokyo 1999.
 T. Ohtsuki,
The perturbative
T. Ohtsuki,
The perturbative 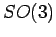 invariant of rational homology
3-spheres recovers from the universal perturbative invariant,
to appear in Topology.
invariant of rational homology
3-spheres recovers from the universal perturbative invariant,
to appear in Topology.
 T. Ohtsuki,
A filtration of the set of integral homology 3-spheres,
Tokyo Institute of Technology preprint, July 1999.
T. Ohtsuki,
A filtration of the set of integral homology 3-spheres,
Tokyo Institute of Technology preprint, July 1999.
 T. Ohtsuki,
Topological quantum field theory for the LMO invariant,
Tokyo Institute of Technology preprint, July 1999.
T. Ohtsuki,
Topological quantum field theory for the LMO invariant,
Tokyo Institute of Technology preprint, July 1999.
 T. Ohtsuki,
Quantum Invariants: A Study of Knots, 3-Manifolds, and their Sets,
Series on Knots and Everything 29, World Scientific, Singapore
2002.
T. Ohtsuki,
Quantum Invariants: A Study of Knots, 3-Manifolds, and their Sets,
Series on Knots and Everything 29, World Scientific, Singapore
2002.
 T. Ohtsuki,
A cabling formula for the 2-loop polynomial of knots,
RIMS (Kyoto) preprint, October 2003, arXiv:math.GT/0310216.
T. Ohtsuki,
A cabling formula for the 2-loop polynomial of knots,
RIMS (Kyoto) preprint, October 2003, arXiv:math.GT/0310216.
 T. Ohtsuki,
Problems on invariants of knots and 3-manifolds,
Invariants of knots and 3-manifolds (Kyoto 2001), Geometry and
Topology Monographs 4 377-572.
T. Ohtsuki,
Problems on invariants of knots and 3-manifolds,
Invariants of knots and 3-manifolds (Kyoto 2001), Geometry and
Topology Monographs 4 377-572.
 Y. Ohyama,
Vassiliev invariants and similarity of knots,
Proc. Amer. Math. Soc. 123 (1995) 287-291.
Y. Ohyama,
Vassiliev invariants and similarity of knots,
Proc. Amer. Math. Soc. 123 (1995) 287-291.
 Y. Ohyama,
Twisting of two strings and Vassiliev invariants,
Topology Appl. 75 (1997) 201-215.
Y. Ohyama,
Twisting of two strings and Vassiliev invariants,
Topology Appl. 75 (1997) 201-215.
 Y. Ohyama,
Remarks on
Y. Ohyama,
Remarks on 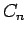 -moves for links and Vassiliev invariants of
order
-moves for links and Vassiliev invariants of
order 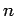 ,
Nagoya Institute of Technology preprint.
,
Nagoya Institute of Technology preprint.
 Y. Ohyama,
Web diagrams and realization of Vassiliev invariants by knots,
Jour. of Knot Theory and Its Ramifications 9(5) (2000) 693-701.
Y. Ohyama,
Web diagrams and realization of Vassiliev invariants by knots,
Jour. of Knot Theory and Its Ramifications 9(5) (2000) 693-701.
 Y. Ohyama and K. Taniyama,
Vassiliev invariants of knots in a spatial graph,
Pacific Journal of Mathematics 200 (2001) 191-205.
Y. Ohyama and K. Taniyama,
Vassiliev invariants of knots in a spatial graph,
Pacific Journal of Mathematics 200 (2001) 191-205.
 Y. Ohyama and T. Tsukamoto,
On Habiro's
Y. Ohyama and T. Tsukamoto,
On Habiro's 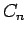 -moves and Vassiliev invariants of order
-moves and Vassiliev invariants of order 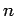 ,
Jour. of Knot Theory and its Ramifications 8(1) (1999) 15-23.
,
Jour. of Knot Theory and its Ramifications 8(1) (1999) 15-23.
 Y. Ohyama and H. Yamada,
Delta and clasp-pass distance and Vassiliev invariants of knots,
Nagoya Institute of Technology and Waseda University preprint, January
2001.
Y. Ohyama and H. Yamada,
Delta and clasp-pass distance and Vassiliev invariants of knots,
Nagoya Institute of Technology and Waseda University preprint, January
2001.
 M. Okamoto,
Vassiliev invariants of type 4 for algebraically split links,
Kobe Jour. of Math. 14-2 (1997) 145-196.
M. Okamoto,
Vassiliev invariants of type 4 for algebraically split links,
Kobe Jour. of Math. 14-2 (1997) 145-196.
 M. Okamoto,
On Vassiliev invariants for algebraically split links,
Jour. of Knot Theory and its Ramifications 7-6 (1998) 807-835.
M. Okamoto,
On Vassiliev invariants for algebraically split links,
Jour. of Knot Theory and its Ramifications 7-6 (1998) 807-835.
 P-Z. Ong and S-W. Yang,
Cohomology of Vassiliev complex and passing product,
National Taiwan University preprint, September 1994.
P-Z. Ong and S-W. Yang,
Cohomology of Vassiliev complex and passing product,
National Taiwan University preprint, September 1994.
 P-Z. Ong and S-W. Yang,
Homology of Vassiliev complex,
National Taiwan University preprint, August 1995.
P-Z. Ong and S-W. Yang,
Homology of Vassiliev complex,
National Taiwan University preprint, August 1995.
 P-Z. Ong and S-W. Yang,
Higher degree Vassiliev invariants: a survey article,
National Taiwan University preprint, September 1995.
P-Z. Ong and S-W. Yang,
Higher degree Vassiliev invariants: a survey article,
National Taiwan University preprint, September 1995.
 T. Ozawa,
Finite order topological invariants of plane curves,
Jour. of Knot Theory and its Ramifications 8(1) (1999) 33-47.
T. Ozawa,
Finite order topological invariants of plane curves,
Jour. of Knot Theory and its Ramifications 8(1) (1999) 33-47.
Sergei DUZHIN
2013-07-04