References beginning with P
 P. Papi and C. Procesi (assisted
by P. Cellini),
Invarianti di nodi,
survey monograph, to appear in Quaderni Dell'U.M.I.
P. Papi and C. Procesi (assisted
by P. Cellini),
Invarianti di nodi,
survey monograph, to appear in Quaderni Dell'U.M.I.
 B. Patureau-Mirand,
Caractères sur l'algèbre de diagrammes trivalents
B. Patureau-Mirand,
Caractères sur l'algèbre de diagrammes trivalents 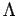 ,
Geometry and Topology 6-20 (2002) 565-607,
arXiv:math.GT/0107137.
,
Geometry and Topology 6-20 (2002) 565-607,
arXiv:math.GT/0107137.
 B. Patureau-Mirand,
Invariant d'entrelacs associé à la représentation des
spineurs de
B. Patureau-Mirand,
Invariant d'entrelacs associé à la représentation des
spineurs de 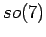 ,
Université Paris 7 preprint, July 2001, arXiv:math.GT/0107138.
,
Université Paris 7 preprint, July 2001, arXiv:math.GT/0107138.
 B. Patureau-Mirand,
Non injectivity of the ``hair'' map,
Université Paris 7 preprint, February 2002, arXiv:math.GT/0202065.
B. Patureau-Mirand,
Non injectivity of the ``hair'' map,
Université Paris 7 preprint, February 2002, arXiv:math.GT/0202065.
 B. Patureau-Mirand,
Quantum link invariant from the Lie superalgebra
B. Patureau-Mirand,
Quantum link invariant from the Lie superalgebra
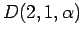 ,
Université de Bretagne-Sud preprint, April 2004,
arXiv:math.GT/0404548.
,
Université de Bretagne-Sud preprint, April 2004,
arXiv:math.GT/0404548.
 R. Picken,
Knot invariants from a Kohno-Kontsevich integral for braids,
q-alg/9707010 preprint, July 1997.
R. Picken,
Knot invariants from a Kohno-Kontsevich integral for braids,
q-alg/9707010 preprint, July 1997.
 S. Piunikhin,
Weights of Feynman diagrams, link polynomials and Vassiliev
knot invariants,
Jour. of Knot Theory and its Ramifications 4(1) (1995) 165-188.
S. Piunikhin,
Weights of Feynman diagrams, link polynomials and Vassiliev
knot invariants,
Jour. of Knot Theory and its Ramifications 4(1) (1995) 165-188.
 S. Piunikhin,
Combinatorial expression for universal Vassiliev link invariant,
Comm. Math. Phys. 168-1 1-22.
S. Piunikhin,
Combinatorial expression for universal Vassiliev link invariant,
Comm. Math. Phys. 168-1 1-22.
 S. Piunikhin,
Addendum to the paper ``Combinatorial expression for universal
Vassiliev link invariant,
November 1993, preprint.
S. Piunikhin,
Addendum to the paper ``Combinatorial expression for universal
Vassiliev link invariant,
November 1993, preprint.
 S. Podkorytov,
Vassiliev invariants of smooth submanifolds,
Abstract of a talk (1998, in Russian).
S. Podkorytov,
Vassiliev invariants of smooth submanifolds,
Abstract of a talk (1998, in Russian).
 S. Podkorytov,
On the maps of a sphere into a simply connected space,
Zapiski POMI, v. 329 (2005), pp. 159-194 (in Russian).
S. Podkorytov,
On the maps of a sphere into a simply connected space,
Zapiski POMI, v. 329 (2005), pp. 159-194 (in Russian).
 S. Poirier,
Rationality results for the configuration space integral of
knots,
Université de Grenoble I preprint, December 1998. See also
math.GT/9901028.
S. Poirier,
Rationality results for the configuration space integral of
knots,
Université de Grenoble I preprint, December 1998. See also
math.GT/9901028.
 S. Poirier,
The limit configuration space integral for tangles and the
Kontsevich integral,
Université de Grenoble I preprint, February 1999,
arXiv:math.GT/9902058.
S. Poirier,
The limit configuration space integral for tangles and the
Kontsevich integral,
Université de Grenoble I preprint, February 1999,
arXiv:math.GT/9902058.
 S. Poirier,
The configuration space integral for links and tangles in
S. Poirier,
The configuration space integral for links and tangles in
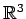 ,
Algebraic
and Geometric Topology, 2-40 (2002) 1001-1050,
arXiv:math.GT/0005085.
,
Algebraic
and Geometric Topology, 2-40 (2002) 1001-1050,
arXiv:math.GT/0005085.
 S. Poirier,
A note on the configuration space integral,
preprint, January 2002.
S. Poirier,
A note on the configuration space integral,
preprint, January 2002.
 M. Polyak,
Link homotopy and Vassiliev knot invariants,
IHES preprint, June 1996.
M. Polyak,
Link homotopy and Vassiliev knot invariants,
IHES preprint, June 1996.
 M. Polyak,
On Milnor's triple linking number,
Comp. Rend. A. S. Paris 325 Serie I (1997), 77-82.
M. Polyak,
On Milnor's triple linking number,
Comp. Rend. A. S. Paris 325 Serie I (1997), 77-82.
 M. Polyak,
Skein relations and Gauss diagram formulas for Milnor's
M. Polyak,
Skein relations and Gauss diagram formulas for Milnor's
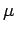 -invariants,
Tel Aviv University preprint, December 1998.
-invariants,
Tel Aviv University preprint, December 1998.
 M. Polyak,
On the algebra of arrow diagrams,
Let. Math. Phys. 51 (2000) 275-291.
M. Polyak,
On the algebra of arrow diagrams,
Let. Math. Phys. 51 (2000) 275-291.
 M. Polyak,
Feynman diagrams for pedestrians and mathematicians,
Technion preprint, June 2004, arXiv:math.GT/0406251.
M. Polyak,
Feynman diagrams for pedestrians and mathematicians,
Technion preprint, June 2004, arXiv:math.GT/0406251.
 M. Polyak and O. Viro,
Gauss diagram formulas for Vassiliev invariants,
Int. Math. Res. Notes 11 (1994) 445-454.
M. Polyak and O. Viro,
Gauss diagram formulas for Vassiliev invariants,
Int. Math. Res. Notes 11 (1994) 445-454.
 M. Polyak and O. Viro,
On the Casson knot invariant,
Jour. of Knot Theory and its Ramifications, to appear,
arXiv:math.GT/9903158.
M. Polyak and O. Viro,
On the Casson knot invariant,
Jour. of Knot Theory and its Ramifications, to appear,
arXiv:math.GT/9903158.
 V. V. Prasolov and A. B. Sossinsky,
Knots, links, braids and 3-manifolds: an introduction to the new
invariants in low-dimensional topology,
Translations of Mathematical Monographs 154, American Mathematical
Society 1997.
V. V. Prasolov and A. B. Sossinsky,
Knots, links, braids and 3-manifolds: an introduction to the new
invariants in low-dimensional topology,
Translations of Mathematical Monographs 154, American Mathematical
Society 1997.
 J. H. Przytycki,
Vassiliev-Gusarov skein modules of 3-manifolds and criteria
for periodicity of knots,
in Low-Dimensional Topology, Knoxville 1992, 143-162,
International Press, Cambridge MA, 1994.
J. H. Przytycki,
Vassiliev-Gusarov skein modules of 3-manifolds and criteria
for periodicity of knots,
in Low-Dimensional Topology, Knoxville 1992, 143-162,
International Press, Cambridge MA, 1994.
 J. H. Przytycki,
Symmetric knots and billiard knots,
Chapter 20 of Ideal Knots, Series on Knots and Everything 19, Eds. A. Stasiak, V. Katrich and L. Kauffman, World
Scientific (1999) 374-414, arXiv:math.GT/0405151.
J. H. Przytycki,
Symmetric knots and billiard knots,
Chapter 20 of Ideal Knots, Series on Knots and Everything 19, Eds. A. Stasiak, V. Katrich and L. Kauffman, World
Scientific (1999) 374-414, arXiv:math.GT/0405151.
 J. H. Przytycki,
Graphs and links,
arXiv:math.GT/0601227.
J. H. Przytycki,
Graphs and links,
arXiv:math.GT/0601227.
 J. H. Przytycki and A. S. Sikora,
Topological insights from the Chinese rings,
Proc. Amer. Math. Soc., to appear,
arXiv:math.GT/0007134.
J. H. Przytycki and A. S. Sikora,
Topological insights from the Chinese rings,
Proc. Amer. Math. Soc., to appear,
arXiv:math.GT/0007134.
 J. H. Przytycki and
K. Taniyama,
The Kanenobu-Miyazawa conjecture and the Vassiliev-Gusarov
skein modules based on mixed crossings,
Proc. Amer. Math. Soc. 129 (2001) 2799-2802.
J. H. Przytycki and
K. Taniyama,
The Kanenobu-Miyazawa conjecture and the Vassiliev-Gusarov
skein modules based on mixed crossings,
Proc. Amer. Math. Soc. 129 (2001) 2799-2802.
Sergei DUZHIN
2013-07-04