1.9 Isotopy Types of Harnack M-Curves

Harnack's construction of M-curves in [Har-76] differs from the construction in the proof of Theorem 1.6.B in that a conic, rather than a curve of degree 5, is used as the original curve. Figure 9 shows that the M-curves of degree $\le 5$ which are used in Harnack's construction [Har-76]. For $m\ge 6$ Harnack's construction gives M-curves with the same isotopy types as in the construction in Section 1.6.

Figure 9:

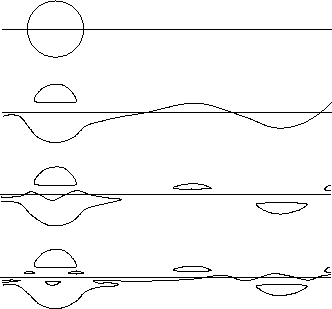
In these constructions one obtains different isotopy types of M-curves depending on the choice of auxiliary curves (more precisely, depending on the relative location of the intersections $\mathbb{R}B_m\cap \mathbb{R}L)$. Recall that in order to obtain M-curves it is necessary for the intersection $\mathbb{R}B_m\cap \mathbb{R}L$ to consist of $m$ points and lie in a single component of the set $\mathbb{R}L\smallsetminus \mathbb{R}B_{m-1}$, where for odd $m$ this component must contain $\mathbb{R}B_{m-2}\cap \mathbb{R}L$. It is easy to see that the isotopy type of the resulting M-curve of degree $m$ depends only on the choice of the components of $\mathbb{R}L\smallsetminus \mathbb{R}B_{r-1}$ for even $r<m$ where the intersections $\mathbb{R}L\cap \mathbb{R}B_r$ are to be found. If we take the components containing $\mathbb{R}L\cap \mathbb{R}B_{r-2}$ for even $r$ as well, then the degree $m$ M-curve obtained from the construction has isotopy type $\langle J\amalg (m^2-3m+2)/2\rangle$ for odd $m$ and $\langle (3m^2-6m)/8\amalg 1\langle (m^2-6m+8)/8\rangle\rangle$ for even $m$. In Table 2 we have listed the isotopy types of M-curves of degree $\le 10$ which one obtains from Harnack's construction using all possible $B_m$.

Table 2:

$m$	Isotopy types of the Harnack M-curves of degree $m$
2	$\langle 1\rangle$
3	$\langle J\amalg 1\rangle$
4	$\langle 4\rangle$
5	$\langle J\amalg 6\rangle$
6	$\langle 9\amalg 1\langle 1\rangle\rangle$
7	$\langle J\amalg 15\rangle\qquad \langle J\amalg 13\amalg 1 \langle 1\rangle\rangle$
8	$\langle 18\amalg 1\langle 3\rangle\rangle\qquad\qquad\qquad \langle 17\amalg 1\langle 1\rangle \amalg 1\langle 2\rangle\rangle$
9	$\langle J\amalg 28\rangle\qquad \langle J\amalg 24\amalg 1\langle 3\rangle\ran... ...qquad \langle J\amalg 23\amalg 1\langle 1\rangle\amalg 1\langle 2\rangle\rangle$
10	$\langle 30\amalg 1\langle 6\rangle\rangle \qquad \langle 29\amalg 2\langle 3\r... ...malg 1\langle 1\rangle \amalg 1\langle 2\rangle \amalg 1\langle 3\rangle\rangle$

In conclusion, we mention two curious properties of Harnack M-curves, for which the reader can easily furnish a proof.

Figure 10: Construction of even degree curves by Hilbert's method. Degrees 4 and 6.

Figure 11: Construction of odd degree curves by Hilbert's method. Degrees 3 and 5.

1.9.A   The depth of a nest in a Harnack M-curve is at most 2.

1.9.B   Any Harnack M-curve of even degree $m$ has $(3m^2-6m+8) /8$ outer ovals and $(m^2-6m+8)/8$ inner ovals.