


Next: 2.7 Rokhlin's Complex Orientation
Up: 2 A Real Algebraic
Previous: 2.5 Digression: Oriented Topological
2.6 The Simplest Restrictions on a Complex Scheme
To begin with, recall the following obvious restriction, which
was used in Section 2.2.
2.6.A
A curve with empty real point set is of type
II.

The next theorem is in a sense dual to 2.6.A.
2.6.B
An M-curve is of type I
.
Proof.
Let
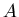
be an M-curve of degree
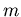
. Then
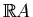
is the union of
disjoint circles
lying on
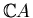
, which is a sphere with
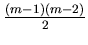
handles. That many disjoint circles necessarily divide a sphere with
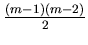
handles. Indeed, cut
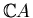
along
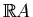
. The Euler
characteristic of a surface has not changed. It equals
Then cap each
boundary circle with a disk. Each component of
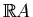
gives rise to 2
boundary circles. Therefore the number of the boundary circles is
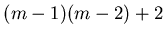
. The surface which is obtained has Euler characteristic
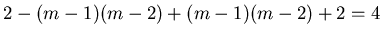
. However, there is no connected closed
surface with Euler characteristic 4. (A connected closed oriented
surface is a sphere with
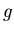
handles for some
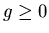
; it has Euler
characteristic
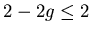
.)

2.6.C Klein's Congruence (see [
Kle-22, page
172])
If
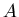
is a curve of type I
of
degree 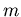 with
with 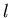 ovals, then
ovals, then
![$ l\equiv [\frac m2]\mod2$](img366.png) .
.
Proof.
Consider a half of
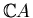
bounded by
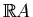
. Its Euler
characteristic equals the half of the Euler characteristic of
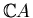
,
i.e.
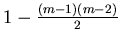
. Cap the boundary components of the half with
disjoint disks. This increases the Euler characteristics by the number
of components of
. In the case of even degree
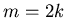
, the Euler
characteristic of the result is
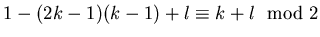
.
In the case of odd degree
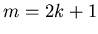
, it is
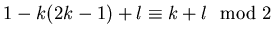
.
In both cases the Euler characteristic should be even, since the
surface is closed orientable and connected (i.e. sphere with handles).
Thus in both cases
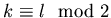
, where
![$ k=[m/2]$](img372.png)
.

2.6.D A Nest of the Maximal Depth
(see [
Rok-78, 3.6]).
A real scheme of degree
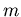
containing a nest of depth
![$ k=[m/2]$](img372.png)
is of type I
.
Such a scheme exists and is unique for any 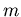 (for even
(for even 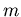 it is
just the nest, for odd
it is
just the nest, for odd 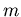 it consists of the nest and the one-sided
component). To realize the scheme, perturb the union of
it consists of the nest and the one-sided
component). To realize the scheme, perturb the union of 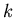 concentric circles and, in the case of odd
concentric circles and, in the case of odd  , a line disjoint from
the circles. The uniqueness was proved in 1.3, see 1.3.C.
, a line disjoint from
the circles. The uniqueness was proved in 1.3, see 1.3.C.
I preface the proof of 2.6.D with a construction interesting for
its own. It provides a kind of window through which one can take a look
at the imaginary part of
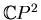 .
.
As we know (see Section 2.2), the complex point set of a real
line is divided by its real point set into two halves, which are in a
natural one-to-one correspondence with the orientations of the real
line. The set of all real lines on the projective plane is the real
point set of the dual projective plane. The halves of lines comprise a
two-dimensional sphere covering this projective plane. An especially
clear picture of these identifications appears, if one identifies real
lines on the projective plane with real planes in
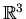 containing 0.
A half of a line is interpreted as the corresponding plane with
orientation. An oriented plane corresponds to its positive unit normal
vector, which is nothing but a point of
containing 0.
A half of a line is interpreted as the corresponding plane with
orientation. An oriented plane corresponds to its positive unit normal
vector, which is nothing but a point of 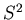 . The complex conjugation
. The complex conjugation
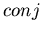 maps a half of a real line to the other half of the same line.
It corresponds to the reversing of the orientation, which, in turn,
corresponds to the antipodal involution
maps a half of a real line to the other half of the same line.
It corresponds to the reversing of the orientation, which, in turn,
corresponds to the antipodal involution
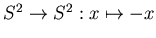 .
.
There is a unique real line passing through any imaginary point of
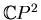 . To construct such a line, connect the point with the conjugate
one. The connecting line is unique since a pair of distinct points
determines a line, and this line is real, since it coincides with its
image under
. To construct such a line, connect the point with the conjugate
one. The connecting line is unique since a pair of distinct points
determines a line, and this line is real, since it coincides with its
image under 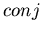 .
.
Consequently, there is a unique half of a real line containing an
imaginary point of
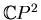 . This construction determines a fibration
. This construction determines a fibration
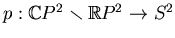 . The fibres of
. The fibres of 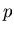 are the halves of real
lines. Note that conjugate points of
are the halves of real
lines. Note that conjugate points of
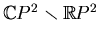 are mapped to
antipodal points of
are mapped to
antipodal points of 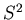 .
.
Proof.
[Proof of
2.6.D] Let
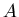
be a real projective curve
of degree
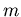
with a nest of depth
![$ [m/2]$](img55.png)
. Choose a point
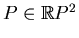
from the domain encircled by the interior oval of the nest. Consider
the great circle of
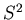
consisting of halves of real lines which pass
through
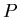
. Since each line passing through
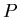
intersects
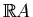
in
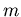
points, it cannot intersect
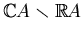
. Therefore the great
circle has no common point with the image of
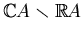
under
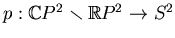
. But the image contains, together with any of
its points, the antipodal point. Therefore it cannot be connected, and
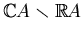
cannot be connected, too.




Next: 2.7 Rokhlin's Complex Orientation
Up: 2 A Real Algebraic
Previous: 2.5 Digression: Oriented Topological
Oleg Viro
2000-12-30
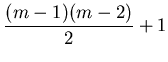
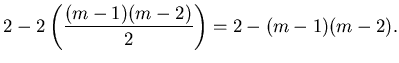
![]() (for even
(for even ![]() it is
just the nest, for odd
it is
just the nest, for odd ![]() it consists of the nest and the one-sided
component). To realize the scheme, perturb the union of
it consists of the nest and the one-sided
component). To realize the scheme, perturb the union of ![]() concentric circles and, in the case of odd
concentric circles and, in the case of odd ![]() , a line disjoint from
the circles. The uniqueness was proved in 1.3, see 1.3.C.
, a line disjoint from
the circles. The uniqueness was proved in 1.3, see 1.3.C.
![]() .
.
![]() containing 0.
A half of a line is interpreted as the corresponding plane with
orientation. An oriented plane corresponds to its positive unit normal
vector, which is nothing but a point of
containing 0.
A half of a line is interpreted as the corresponding plane with
orientation. An oriented plane corresponds to its positive unit normal
vector, which is nothing but a point of ![]() . The complex conjugation
. The complex conjugation
![]() maps a half of a real line to the other half of the same line.
It corresponds to the reversing of the orientation, which, in turn,
corresponds to the antipodal involution
maps a half of a real line to the other half of the same line.
It corresponds to the reversing of the orientation, which, in turn,
corresponds to the antipodal involution
![]() .
.
![]() . To construct such a line, connect the point with the conjugate
one. The connecting line is unique since a pair of distinct points
determines a line, and this line is real, since it coincides with its
image under
. To construct such a line, connect the point with the conjugate
one. The connecting line is unique since a pair of distinct points
determines a line, and this line is real, since it coincides with its
image under ![]() .
.
![]() . This construction determines a fibration
. This construction determines a fibration
![]() . The fibres of
. The fibres of ![]() are the halves of real
lines. Note that conjugate points of
are the halves of real
lines. Note that conjugate points of
![]() are mapped to
antipodal points of
are mapped to
antipodal points of ![]() .
.