2.7 Rokhlin's Complex Orientation Formula

Now we shall consider a powerful restriction on a complex orientation of a curve of type I. It is powerful enough to imply restrictions even on real schemes of type I. The first version of this restriction was published in 1974, see [Rok-74]. There Rokhlin considered only the case of an algebraic M-curve of even degree. In [Mis-75] Mishachev considered the case of an algebraic M-curve of odd degree. For an arbitrary nonsingular algebraic curve of type I, it was formulated by Rokhlin [Rok-78] in 1978. The proofs from [Rok-74] and [Mis-75] work in this general case. The only reason to restrict the main formulations in these early papers to M-curves was the traditional viewpoint on the subject of the topology of real plane algebraic curves.

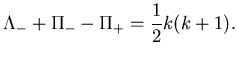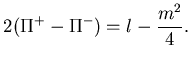
Here are Rokhlin's formulations from [Rok-78].

2.7.A Rokhlin Formula.   If the degree $m$ is even and the curve is of type I, then

$$2(\Pi^+-\Pi^-)=l-\frac{m^2}4.$$

2.7.B Rokhlin-Mishachev Formula.   If $m$ is odd and the curve is of type I, then

$$\Lambda^+-\Lambda^-+2(\Pi^+-\Pi^-)=l-\frac{m^2-1}4.$$

Theorems 2.7.A and 2.7.B can be united into a single formulation. This requires, however, two preliminary definitions.

First, given an oriented topological curve $C$ on $\mathbb{R}P^2$, for any point $x$ of its complement, there is the index $i_C(x)$ of the point with respect to the curve. It is a nonnegative integer defined as follows. Draw a line $L$ on $\mathbb{R}P^2$ through $x$ transversal to $C$. Equip it with a normal vector field vanishing only at $x$. For such a vector field, one may take the velocity field of a rotation of the line around $x$. At each intersection point of $L$ and $C$ there are two directions transversal to $L$: the direction of the vector belonging to the normal vector field and the direction defined by the local orientation of $C$ at the point. Denote the number of intersection points where the directions are faced to the same side of $L$ by $i_+$ and the number of intersection points where the directions are faced to the opposite sides of $L$ by $i_-$. Then put $i_C(x)=\vert i_+-i_-\vert/2$.⁵ It is easy to check that $i_C(x)$ is well defined: it depends neither on the choice of $L$, nor on the choice of the normal vector field. It does not change under reversing of the orientation of $C$. Thus for any nonsingular curve $A$ of type I on the complement $\mathbb{R}P^2\smallsetminus \mathbb{R}A$, one has well defined function $i_{\mathbb{R}A}$.

The second prerequisite notion is a sort of unusual integration: an integration with respect to the Euler characteristic, in which the Euler characteristic plays the role of a measure. It is well known that the Euler characteristic shares an important property of measures: it is additive in the sense that for any sets $A$, $B$ such that the Euler characteristics $\chi A$, $\chi B$, $\chi(A\cap B)$ and $\chi(A\cup B)$ are defined,

$$\chi(A\cup B)=\chi(A) +\chi(B)-\chi(A\cap B).$$

However, the Euler characteristic is neither $\sigma$-additive, nor positive. Thus the usual theory of integral cannot be applied to it. This can be done though if one restricts to a very narrow class of functions. Namely, to functions which are finite linear combinations of characteristic functions of sets belonging to some algebra of subsets of a topological space such that each element of the algebra has a well defined Euler characteristic. For a function $f=\sum_{i=1}^{r}\lambda _i\hbox{\rm\rlap {1}\hskip.03in{{\rm I}}}_{S_i}$ set

$$\int f(x) d\chi(x)=\sum_{i=1}^{r}\lambda _i\chi(S_i).$$

For details and applications of that notion, see [Vir-88].

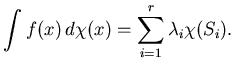
Now we can unite 2.7.A and 2.7.B:

2.7.C Rokhlin Complex Orientation Formula.   If $A$ is a nonsingular real plane projective curve of type I and degree $m$ then

$$\int (i_{\mathbb{R}A}(x))^2 d\chi(x)=\frac{m^2}4.$$

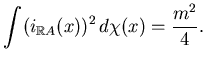
Here I give a proof of 2.7.C, skipping the most complicated details. Take a curve $A$ of degree $m$ and type I. Let $\mathbb{C}A_+$ be its half bounded by $\mathbb{R}A$. It may be considered as a chain with integral coefficients. The boundary of this chain (which is $\mathbb{R}A$ equipped with the complex orientation) bounds in $\mathbb{R}P^2$ a chain $c$ with rational coefficients, since $H_1(\mathbb{R}P^2; \mathbb{Q})=0$. In fact, in the case of even degree the chain can be taken with integral coefficients, but in the case of odd degree the coefficients are necessarily half-integers. The explicit form of $c$ may be given in terms of function $i_{\mathbb{R}A}$: it is a linear combination of the fundamental cycles of the components of $\mathbb{R}P^2\smallsetminus \mathbb{R}A$ with coefficients equal to the values of $i_{\mathbb{R}A}$ on the components (taken with appropriate orientations).

Now take the cycle $[\mathbb{C}A_+]-c$ and its image under $conj$, and calculate their intersection number in two ways.

First, it is easy to see that the homology class $\xi$ of $[\mathbb{C}A_+]-c$ is equal to $\frac12[\mathbb{C}A]=\frac m2[\mathbb{C}P^1]\in H_2(\mathbb{C}P^2; \mathbb{Q})$. Indeed, $[\mathbb{C}A_+]-c-conj([\mathbb{C}A_+]-c)=[\mathbb{C}A]+c-conj(c)=[\mathbb{C}A]$, and therefore $\xi-conj_*(\xi)=[\mathbb{C}A]=m[\mathbb{C}P^1]\in H_2(\mathbb{C}P^2)$. On the other hand, $conj$ acts in $H_2(\mathbb{C}P^2)$ as multiplication by $-1$, and hence $\xi-conj_*(\xi)=2\xi=m[\mathbb{C}P^1]$. Therefore $\xi\circ conj_*(\xi)=-(\frac m2)^2$.

Second, one may calculate the same intersection number geometrically: moving the cycles into a general position and counting the local intersection numbers. I will perturb the cycle $[\mathbb{C}A_+]-c$. First, choose a smooth tangent vector field $V$ on $\mathbb{R}P^2$ such that it has only nondegenerate singular points, the singular points are outside $\mathbb{R}A$, and on $\mathbb{R}A$ the field is tangent to $\mathbb{R}A$ and directed according to the complex orientation of $A$ which comes from $\mathbb{C}A_+$. The latter means that at any point $x\in\mathbb{R}A$ the vector $\sqrt{-1}V(x)$ is directed inside $\mathbb{C}A_+$ (the multiplication by $\sqrt{-1}$ makes a real vector normal to the real plane and lieves any vector tangent to $\mathbb{R}A$ tangent to $\mathbb{C}A$). Now shift $\mathbb{R}A$ inside $\mathbb{C}A_+$ along $\sqrt{-1}V$ and extend this shift to a shift of the whole chain $c$ along $\sqrt{-1}V$. Let $c'$ denote the result of the shift of $c$ and $h$ denote the part of $\mathbb{C}A_+$ which was not swept during the shift. The cycle $[h]-c'$ represents the same homology class $\xi$ as $[\mathbb{C}A_+]-c$, and we can use it to calculate the intersection number $\xi\circ conj_*(\xi)$. The cycles $[h]-c'$ and $conj([\mathbb{C}A_+]-c)$ intersect only at singular points of $V$. At a singular point $x$ they are smooth transversal two-dimensional submanifolds, each taken with multiplicity $-i_{\mathbb{R}A}(x)$. The local intersection number at $x$ is equal to $(i_{\mathbb{R}A}(x))^2$ multiplied by the local intersection number of the submanifolds supporting the cycles. The latter is equal to the index of the vector field $V$ at $x$ multiplied by $-1$.

I omit the proof of the latter statement. It is nothing but a straightforward checking that multiplication by $\sqrt{-1}$ induces isomorphism between tangent and normal fibrations of $\mathbb{R}A$ in $\mathbb{C}A$ reversing orientation.

Now recall that the sum of indices of a vector field tangent to the boundary of a compact manifold is equal to the Euler characteristic of the manifold. Therefore the input of singular points lying in a connected component of $\mathbb{R}P^2\smallsetminus \mathbb{R}A$ is equal to the Euler characteristic of the component multiplied by $-(i_{\mathbb{R}A}(x))^2$ for any point $x$ of the component. Summation over all connected components of $\mathbb{R}P^2\smallsetminus \mathbb{R}A$ gives $-\int(i_{\mathbb{R}A}(x))^2 d\chi(x)$. Its equality to the result of the first calculation is the statement of 2.7.C.$\qedsymbol$

2.7.D Corollary 1. Arnold Congruence.   For a curve of an even degree $m=2k$ and type I

$$p-n\equiv k^2\mod4.$$

Proof. Observe that in the case of an even degree $i_{\mathbb{R}A}(x)$ is even, iff $x\in\mathbb{R}P^2_+$. Therefore

$$(i_{\mathbb{R}A}(x))^2\equiv\begin{cases}0\mod4, \text{ if } x\in\mathbb{R}P^2_+\\ 1\mod4, \text{ if } x\in\mathbb{R}P^2_-.\end{cases}$$

Thus

$$\int_{\mathbb{R}P^2}(i_{\mathbb{R}A}(x))^2 d\chi(x)\equiv\chi(\mathbb{R}P^2_+)\mod4.$$

Recall that $\chi(\mathbb{R}P^2_+ )=p-n$, see 1.11. Hence the left hand side of Rokhlin's formula is $p-n$ modulo 4. The right hand side is $k^2$. $\qedsymbol$

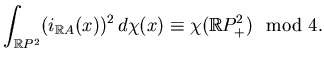
Denote the number of all injective pairs of ovals for a curve under consideration by $\Pi$.

2.7.E Corollary 2.   For any curve of an even degree $m=2k$ and type I with $l$ ovals

$$\Pi\ge\frac12\vert l-k^2\vert.$$

Proof. By 2.7.A $\Pi^+-\Pi_-=\frac12(l-k^2)$. On the other hand, $\Pi=\Pi_++\Pi_-\ge\vert\Pi_+-\Pi_-\vert$. $\qedsymbol$

2.7.F Corollary 3.   For any curve of an odd degree $m=2k+1$ and type I with $l$ ovals

$$\Pi+l\ge \frac12k(k+1).$$

Proof. Since $l=\Lambda _++\Lambda _-$, the Rokhlin - Mishachev formula 2.7.B can be rewritten as follows:

$$\Lambda _-+\Pi_-\Pi_+=\frac12k(k+1).$$

On the other hand, $\Pi\ge\Pi_-\Pi_+$ and $l\ge\Lambda _-$. $\qedsymbol$