In each area of mathematics there are objects which appear much more frequently than other ones. Some of them (like Dynkin diagrams) appear in several domains quite distant from each other. In topology of real plane algebraic curves Harnack curves play this role. It was not an accident that they were constructed in the first paper devoted to this subject. Whenever one tries to construct an M-curve, the first success provides a Harnack curve. Patchwork construction is no exception to the rule.
In this section we describe, using the Patchwork Theorem,
the construction of some Harnack curves of an even degree ![]() .
.
In what follows all the triangulations satisfy an additional assumption: they are primitive which means that all triangles are of area 1/2 (or, equivalently, that all integer points of the triangulated area are vertices of the triangulation). A polynomial defining a T-curve contains the maximal collection of nonzero monomials if and only if the triangulation used in the construction of the T-curve is primitive.
A primitive convex triangulation of ![]() is said to be equipped with
a Harnack distribution of signs if:
is said to be equipped with
a Harnack distribution of signs if:
vertexhas the sign "-", if
are both even, and has the sign "+" in the opposite case.
A vertex ![]() of a triangulation of
of a triangulation of ![]() is called even
if
is called even
if ![]() are both even, and odd if not.
are both even, and odd if not.
An example of the construction under consideration is shown in Figure 7.
Proof of Proposition. First, remark that the
number of interior (i. e., lying in the interior of the triangle ![]() )
integer points is equal to
)
integer points is equal to
![]() , the number of
even interior points is equal to
, the number of
even interior points is equal to
![]() , and the
number of odd interior points is equal to
, and the
number of odd interior points is equal to
![]() .
.
Take an arbitrary even interior vertex of a triangulation
of the triangle ![]() . This vertex has the sign "-". All adjacent vertices
(i.e. the vertices connected with the vertex by edges of
the triangulation) are odd, and thus they all have the sign "+".
This means that the star of an even interior vertex contains
an oval of the curve
. This vertex has the sign "-". All adjacent vertices
(i.e. the vertices connected with the vertex by edges of
the triangulation) are odd, and thus they all have the sign "+".
This means that the star of an even interior vertex contains
an oval of the curve ![]() . The number of such ovals is equal to
. The number of such ovals is equal to
![]() .
.
Take now an odd interior vertex of the triangulation. It has
the sign "+".
There are two vertices with "-" and one vertex
with "+" among the images of the vertex
under
![]() and
and
![]() (recall that
(recall that
![]() are reflections with respect to the coordinate axes).
Consider the image with the sign "+".
It is easy to verify, that all its adjacent vertices
have the sign "-".
Again this means that the star of this vertex contains
an oval of the curve
are reflections with respect to the coordinate axes).
Consider the image with the sign "+".
It is easy to verify, that all its adjacent vertices
have the sign "-".
Again this means that the star of this vertex contains
an oval of the curve ![]() . The number of such ovals is equal to
. The number of such ovals is equal to
![]() .
.
Thus
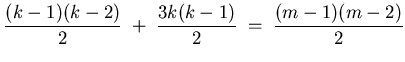
To finish the proof, we need only note that the union of the segments
ARRAY(0x8cc51c0)