a) there exists a nonsingular real algebraic plane projective curve
of degree ![]() with
with
![$\displaystyle p = \frac{3k(k-1)}{2} + 1+
\left[\frac{(k - 3)^2 + 4}{8} \right]$](img111.png)
b) there exists a nonsingular real algebraic plane projective curve
of degree ![]() with
with
![$\displaystyle n = \frac{3k(k-1)}{2} +
\left[\frac{(k - 3)^2 + 4}{8} \right] $](img112.png)
The following theorem gives counter-examples to the Ragsdale Conjecture (or the conjecture of Petrovsky) (cf. [8]).
a) there exists a nonsingular real algebraic plane projective curve
of degree ![]() with
with
![$\displaystyle p = \frac{3k(k-1)}{2} + 1+
\left[\frac{(k - 3)^2 + 4}{8} \right]$](img111.png)
b) there exists a nonsingular real algebraic plane projective curve
of degree ![]() with
with
![$\displaystyle n = \frac{3k(k-1)}{2} +
\left[\frac{(k - 3)^2 + 4}{8} \right] $](img112.png)
Remarks
The term
![$ \left[\frac{(k - 3)^2 + 4}{8} \right]$](img113.png) is positive
when
is positive
when ![]() (i. e.,
the first counter-examples to the Ragsdale Conjecture appear
in degree 10; the patchwork of them is shown in Figures 2
and 3). On the other hand, it is known that there is no
counter-example to the Ragsdale Conjecture among curves of lower degree.
These counter-examples of degree 10 have the real schemes shown in
Figure 8. One of these counter-examples can be improved
in order to obtain a curve of degree 10 with
(i. e.,
the first counter-examples to the Ragsdale Conjecture appear
in degree 10; the patchwork of them is shown in Figures 2
and 3). On the other hand, it is known that there is no
counter-example to the Ragsdale Conjecture among curves of lower degree.
These counter-examples of degree 10 have the real schemes shown in
Figure 8. One of these counter-examples can be improved
in order to obtain a curve of degree 10 with ![]() .
The corresponding patchworks (for
.
The corresponding patchworks (for ![]() and
and ![]() )
are shown in Figures
2 and 3.
)
are shown in Figures
2 and 3.
Recently B. Haas [4] improved the construction presented below
and obtained T-curves of degree ![]() with
with
![$\displaystyle p=\frac{3k(k-1)}{2}+1+\left[\frac{k^2-7k+16}{6}\right].$](img118.png)
Neither the counter-examples provided by the above theorem, nor curves constructed by Haas are M-curves. Moreover, as we mentioned above, it is not known if the conjecture of Petrovsky holds for M-curves. The only known counter-examples to the Ragsdale Conjecture among M-curves are the curves constructed by Viro [16] (see also [18]). It is curious that we did not succeed in presenting those M-counter-examples as T-curves.
Suppose that the hexagon ![]() shown in Figure 9 is placed
inside of the triangle
shown in Figure 9 is placed
inside of the triangle ![]() in such a way that the center of
in such a way that the center of ![]() has both coordinates odd.
Any convex primitive triangulation of a convex part of a convex polygon
is extendable to a convex primitive triangulation of the polygon.
Inside of the hexagon
has both coordinates odd.
Any convex primitive triangulation of a convex part of a convex polygon
is extendable to a convex primitive triangulation of the polygon.
Inside of the hexagon ![]() , let us
take the convex primitive triangulation
shown in Figure 9 and extend it
to
, let us
take the convex primitive triangulation
shown in Figure 9 and extend it
to ![]() .
.
To apply the Patchwork Theorem we need to choose signs at the vertices.
Inside of ![]() put signs according to Figure 9; outside
use the Harnack rule of distribution of signs.
put signs according to Figure 9; outside
use the Harnack rule of distribution of signs.
It is easy to calculate that the corresponding
piecewise-linear curve
![]() has exactly one even oval more than
the Harnack curve constructed above (i. e. now
has exactly one even oval more than
the Harnack curve constructed above (i. e. now
![]() ). One can verify that the curve obtained has the real scheme shown
in Figure 10.
). One can verify that the curve obtained has the real scheme shown
in Figure 10.
Consider the partition of the triangle ![]() shown in Figure 11.
Let us take in each shadowed hexagon the triangulation and the signs
of the hexagon
shown in Figure 11.
Let us take in each shadowed hexagon the triangulation and the signs
of the hexagon ![]() . The triangulation of the union of the shadowed
hexagons can be extended to the primitive convex triangulation
of
. The triangulation of the union of the shadowed
hexagons can be extended to the primitive convex triangulation
of ![]() . Let us fix such an extension. Outside of the union of the
shadowed hexagons choose the signs at the vertices of the triangulation
using the Harnack rule.
. Let us fix such an extension. Outside of the union of the
shadowed hexagons choose the signs at the vertices of the triangulation
using the Harnack rule.
Calculation shows that for the corresponding
piecewise-linear curve
![]()
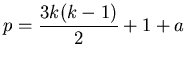
![$\displaystyle a = \left[\frac{(k - 3)^2 + 4}{8} \right]$](img124.png)
To prove part b) of the theorem,
let us take again the partition of the triangle ![]() shown in Figure
11 with the triangulation and the signs of each shadowed hexagon
coinciding with the triangulation and the signs of
shown in Figure
11 with the triangulation and the signs of each shadowed hexagon
coinciding with the triangulation and the signs of ![]() .
Fix, in addition,
a triangulation of a neighborhood of the axis
.
Fix, in addition,
a triangulation of a neighborhood of the axis ![]() and the signs
at the vertices of the triangulation as shown in Figure 13
(the case
and the signs
at the vertices of the triangulation as shown in Figure 13
(the case
![]() ).
The chosen triangulation of the union of the shadowed
hexagons and the neighborhood of the
).
The chosen triangulation of the union of the shadowed
hexagons and the neighborhood of the ![]() -axis can be extended to a
primitive convex triangulation of
-axis can be extended to a
primitive convex triangulation of ![]() . Outside of the union of the
shadowed hexagons and the neighborhood of the
. Outside of the union of the
shadowed hexagons and the neighborhood of the ![]() -axis let us again
choose the signs at the vertices of the triangulation using the Harnack
rule.
-axis let us again
choose the signs at the vertices of the triangulation using the Harnack
rule.
The corresponding piecewise-linear curve
![]() has the real scheme
shown in Figure 14. In this case
has the real scheme
shown in Figure 14. In this case
![]() .
.
![]()