
Here are family
links to
Tatjana Mneva
and
Pavel Mnev
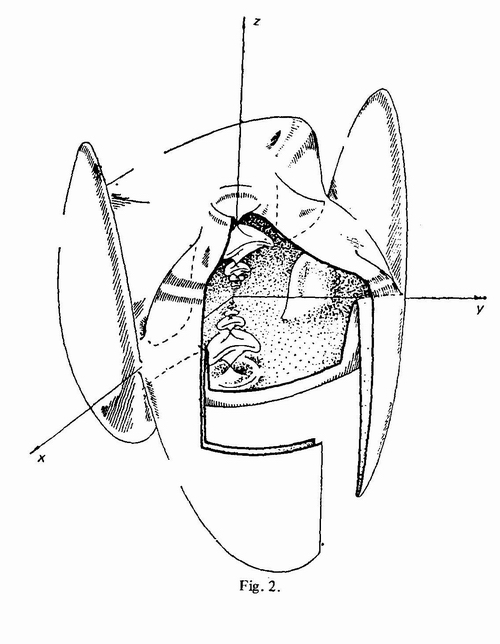
Nikolai Mnev, "Minimal triangulations of circle bundles, circular permutations and binary Chern cocycle"
Nikolai Mnev, "Which circle bundles can be triangulated over $\partial \Delta^3$?"
Nikolai Mnev, "A note on a local combinatorial formula for the Euler class of a PL spherical fiber bundle"
N. Mnev, G. Sharygin, "On local combinatorial formulas for Chern classes of triangulated circle bundle" N. Mnev
On D.K. Biss' papers "The homotopy type of the matroid Grassmannian" and "Oriented matroids, complex manifolds, and a combinatorial model for BU" arXiv:0709.1291 [math.CO]
( As for March 2009, Daniel's errata are accepted for publication. In Annals. I have heard that it will be published at July 2009. In Advances, see also )
"N. Mnev "Combinatorial fiber-bundles and fragmentation of fiberwise homeomorphism" Zapiski Nauchnyh Seminarov POMI ,v344, p 56-173, 2007 (Russian)
arXiv:0708.4039 [math.GT] (English). English verision is published in Journal of Mathematical Sciences Vol 145 No 3, 2007.
N. Mnev "Tangent bundle and Gauss functor of a combinatorial manifold" math.GT/0609257
Correction on announcement:
L.Anderson, N.Mnev "Triangulations of manifolds and combinatorial bundle theory: announcement",
Zap. Nauchn. Sem. POMI v. 267 (2000)
N. Mnev "On the Topology of Cycles in Pseudolinear Programs"
Zap. Nauchn. Sem POMI v. 280 (2001)
L.Anderson, N.Mnev "Triangulations of manifolds and combinatorial bundle theory: announcement",љ
Zap. Nauchn. Sem. POMI v. 267 (2000)
H. Lombardi, N. Mnev and M.-F. Roy, The Positivstellensatz and small deduction rules for
systems of inequalities, Math. Nachr. {\bf 181} (1996), 245--259; MR 97h:14077
A. I. Barvinok, A. M. Vershik and N. E. Mn\"ev, Topology of configuration spaces, of convex polyhedra and of representations of lattices, (Russian) Trudy Mat. Inst. Steklov. {\bf 193} (1992), ; ; translation in Proc. Steklov Inst. Math. {\bf 1993}, no.~3
N. E. Mn\"ev and G. M. Ziegler, Combinatorial models for the finite-dimensional
Grassmannians, Discrete Comput. Geom. {\bf 10} (1993), no.~3, 241--250; MR 94g:52016
N. E. Mn\"ev and J. Richter-Gebert, Two constructions of oriented matroids with disconnected extension space, Discrete Comput. Geom. {\bf 10} (1993), no.~3, 271--285;
N. Mn\"ev, The universality theorem on the oriented matroid stratification of the space
of real matrices, in {\it Discrete and computational geometry (New Brunswick, NJ,
1989/1990)}, 237--243, Amer. Math. Soc., Providence, RI, Providence, RI, 1991; MR
93d:14086
N. E. Mn\"ev, The universality theorems on the classification problem of configuration
varieties and convex polytopes varieties, in {\it Topology and geometry---Rohlin
Seminar}, 527--543, Lecture Notes in Math., 1346, Springer, Berlin-New York, Berlin,
1988; MR 90a:52013
Н.Е. Мнeв, "Топология многообразий комбинаторных типов проективных конфигураций
и выпуклых многогранников",
кандидатская диссертация, 116 стр., Ленинград, 1986
(N. E. Mn\"ev, The topology of configuration varieties and convex polytopes varieties,
PHD thesis, 116 pp., Leningrad, 1986) (Russian, scaned typewritten manuscript 4,7MB)
N. E. Mn\"ev, Varieties of combinatorial types of projective configurations and convex
polyhedra, Dokl. Akad. Nauk SSSR {\bf 283} (1985), no.~6, 1312--1314; MR 87f:52010
N. E. Mn\"ev, The structure of the set of Pareto-critical points of a smooth mapping,
Uspekhi Mat. Nauk {\bf 40} (1985), no.~6(246), 151--152; MR 87c:58032
polytopes, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) {\bf 123}
(1983), 203--207; MR 84m:52012
Also managing
fizmatclub.spb.ru
Here is a brief history of the universality theorem for moduli spaces of line arrangements
Here is something related to
local combinatorics of fiber bundels (targeting to local combinatorics of characteristic classes).
This my subject didn't find public interest,
but i still continue for personal interest.
Steklov Institute of Mathematics at St.Petersburg,
27 Fontanka
St.Petersburg 191011
Russia
e-mail: mnev@pdmi.ras.ru,
@pdmi address can be not available from some domains due to geopolitics, please use
nikolai.mnev@gmail.com
