1.12 Generalizations of Harnack's and Hilbert's Methods. Brusotti. Wiman

Ragsdale's work [Rag-06] was partly inspired by the erroneous paper of Hulbrut, containing a proof of the false assertion that an M-curve can be obtained by means of a classical small perturbation (see Section 1.5) from only two M-curves, one of which must have degree $\le 2$. If this had been true, it would have meant that an inductive construction of M-curves by classical small perturbations starting with curves of small degree must essentially be either Harnack's method or Hilbert's method.

In 1910-1917, L. Brusotti showed that this is not the case. He found inductive constructions of M-curves based on classical small perturbation which were different from the methods of Harnack and Hilbert.

Before describing Brusotti's constructions, we need some definitions. A simple arc $X$ in the set of real points of a curve $A$ of degree $m$ is said to be a base of rank $\rho$ if there exists a curve of degree $\rho$ which intersects the arc in $\rho m$ (distinct) points. A base of rank $\rho$ is clearly also a base of rank any multiple of $\rho$ (for example, one can obtain the intersecting curve of the corresponding degree as the union of several copies of the degree $\rho$ curve, each copy shifted slightly).

An M-curve $A$ is called a generating curve if it has disjoint bases $X$ and $Y$ whose ranks divide twice the degree of the curve. An M-curve $A_0$ of degree $m_0$ is called an auxiliary curve for the generating curve $A$ of degree $m$ with bases $X$ and $Y$ if the following conditions hold:

a) The intersection $\mathbb{R}A\cap \mathbb{R}A_0$ consist of $mm_0$ distinct points and lies in a single component $K$ of $\mathbb{R}A$ and in a single component $K$ of $\mathbb{R}A_0$.

b) The cyclic orders determined on the intersection $\mathbb{R}A\cap \mathbb{R}A_0$ by how it is situated in $K$ and in $K_0$ are the same.

c) $X\subset \mathbb{R}A\smallsetminus \mathbb{R}A_0$.

d) If $K$ is a one-sided curve and $m_0\equiv\mod 2$, then the base $X$ lies outside the oval $K_0$.

e) The rank of the base $X$ is a divisor of the numbers $m+m_0$ and $2m$, and the rank of $Y$ is a divisor of $2m+m_0$ and $2m$.

An auxiliary curve can be the empty curve of degree 0. In this case the rank of $X$ must be a divisor of the degree of the generating curve.

Let $A$ be a generating curve of degree $m$, and let $A_0$ be a curve of degree $m_0$ which is an auxiliary curve with respect to $A$ and the bases $X$ and $Y$. Since the rank of $X$ divides $m+m_0$, we may assume that the rank is equal to $m+m_0$. Let $C$ be a real curve of degree $m+m_0$ which intersects $X$ in $m(m+m_0)$ distinct points. It is not hard to verify that a classical small perturbation of the curve $A\cup A_0$ directed to $L$ will give an M-curve of degree $m+m_0$, and that this M-curve will be an auxiliary curve with respect to $A$ and the bases obtained from $Y$ and $X$ (the bases must change places). We can now repeat this construction, with $A_0$ replaced by the curve that has just been constructed. Proceeding in this way, we obtain a sequence of M-curves whose degree forms an arithmetic progression: $km+m_0$ with $k=1,2,\dotsc$. This is called the construction by Brusotti's method, and the sequence of M-curves is called a Brusotti series.

Any simple arc of a curve of degree $\le 2$ is a base of rank 1 (and hence of any rank). This is no longer the case for curves of degree $\le 3$. For example, an arc of a curve of degree 3 is a base of rank 1 if and only if it contains a point of inflection. (We note that a base of rank 2 on a curve of degree 3 might not contain a point of inflection: it might be on the oval rather than on the one-sided component where all of the points of inflection obviously lie. A curve of degree 3 with this type of base of rank 2 can be constructed by a classical small perturbation of a union of three lines.)

If the generating curve has degree 1 and the auxiliary curve has degree 2, then the Brusotti construction turns out to be Harnack's construction. The same happens if we take an auxiliary curve of degree 1 or 0. If the generating curve has degree 2 and the auxiliary curve has degree 1 or 2 (or 0), then the Brusotti construction is the same as Hilbert's construction.

In general, not all Harnack and Hilbert constructions are included in Brusotti's scheme; however, the Brusotti construction can easily be extended in such a way as to be a true generalization of the Harnack and Hilbert constructions. This extension involves allowing the use of an arbitrary number of bases of the generating curve. Such an extension is particularly worthwhile when the generating curve has degree $\le 2$, in which case there are arbitrarily many bases.

It can be shown that Brusotti's construction with generating curve of degree 1 and auxiliary curve of degree $\le 4$ gives the same types of M-curves as Harnack's construction. But as soon as one uses auxiliary curves of degree 5, one can obtain new isotopy types from Brusotti's construction. It was only in 1971 that Gudkov [Gud-71] found an auxiliary curve of degree 5 that did this. His construction was rather complicated, and so I shall only give some references [Gud-71], [Gud-74], [A'C-79] and present Figure 12, which illustrates the location of the degree 5 curve relative to the generating line.

Figure 12:

Figure 13:

Even with the first stage of Brusotti's construction, i.e., the classical small perturbation of the union of the curve and the line, one obtains an M-curve (of degree 6) which has isotopy type $\langle 5\amalg 1\langle5\rangle\rangle$, an isotopy type not obtained using the constructions of Harnack and Hilbert. Such an M-curve of degree 6 was first constructed in a much more complicated way by Gudkov [GU-69], [Gud-73] in the late 1960's.

In Figures 13 and 14 we show the construction of two curves of degree 6 which are auxiliary curves with respect to a line. In this case the Brusotti construction gives new isotopy types beginning with degree 8.

Figure 14: In the construction by Hilbert's method, we keep track of the locations relative to a fixed line $A$. The union of two conics is perturbed in direction to a $4$-tuple of lines. A curve of degree $4$ is obtained. We add one of the original conics to this curve, and then perturb the union.

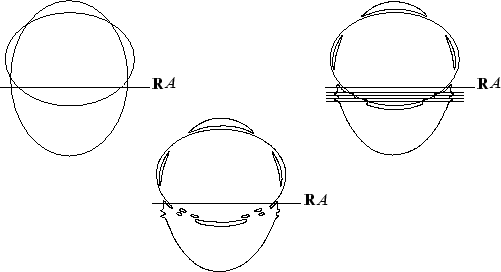In the Hilbert construction we keep track of the location relative to a fixed line $A$. The union of two conics is perturbed in direction to a quadruple of lines. One obtains a curve of degree 4. To this curve one then adds one of the original conics, and the union is perturbed.

In numerous papers by Brusotti and his students, many series of Brusotti M-curves were found. Generally, new isotopy types appear in them beginning with degree 9 or 10. In these constructions they paid much attention to combinations of nests of different depths--a theme which no longer seems to be very interesting. An idea of the nature of the results in these papers can be obtained from Gudkov's survey [Gud-74]; for more details, see Brusotti's survey [Bru-56] and the papers cited there.

An important variant of the classical constructions of M-curves, of which we shall need to make use in the next section, is not subsumed under Brusotti's scheme even in its extended form. This variant, proposed by Wiman [Wim-23], consists in the following. We take an M-curve $A$ of degree $k$ having base $X$ of rank dividing $k$; near this curve we construct a curve $A'$ transversally intersecting $A$ in $k^2$ points of $X$, after which we can subject the union $A\cup A'$ to a classical small perturbation, giving an M-curve of degree $2k$ (for example, a perturbation in direction to an empty curve of degree $2k)$. The resulting M-curve has the following topological structure: each of the components of the curve $A$ except for one (i.e., except for the component containing $X)$ is doubled, i.e., is replaced by a pair of ovals which are each close to an oval of the original curve, and the component containing $X$ gives a chain of $k^2$ ovals. This new curve does not necessarily have a base, so that in general one cannot construct a series of M-curves in this way.