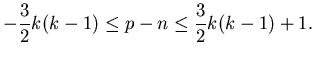1.13 The First Prohibitions not Obtained from Bézout's Theorem

The techniques discussed above are, in essence, completely elementary. As we saw (Section 1.4), they are sufficient to solve the isotopy classification problem for nonsingular projective curves of degree $\le 5$. However, even in the case of curves of degree 6 one needs subtler considerations. Not all of the failed attempts to construct new isotopy types of M-curves of degree 6 (after Hilbert's 1891 paper [Hil-91], there were two that had not been realized: $\langle 9\amalg 1\langle 1\rangle\rangle$ and $\langle 1\amalg 1 \langle 9\rangle\rangle)$ could be explained on the basis of Bézout's theorem. Hilbert undertook an attack on M-curves of degree 6. He was able to grope his way toward a proof that isotopy types cannot be realized by curves of degree 6, but the proof required a very involved investigation of the natural stratification of the space $\mathbb{R}C_6$ of real curves of degree 6. In [Roh-13], Rohn, developing Hilbert's approach, proved (while stating without proof several valid technical claims which he needed) that the types $\langle 11\rangle$ and $\langle 1\langle 10\rangle\rangle$ cannot be realized by curves of degree 6. It was not until the 1960's that the potential of this approach was fully developed by Gudkov. By going directly from Rohn's 1913 paper [Roh-13] to the work of Gudkov, I would violate the chronological order of my presentation of the history of prohibitions. But in fact I would only be omitting one important episode, to be sure a very remarkable one: the famous work of I. G. Petrovsky [Pet-33], [Pet-38] in which he proved the first prohibition relating to curves of arbitrary even degree and not a direct consequence of Bézout's theorem.

1.13.A (Petrovsky Theorem ([Pet-33], [Pet-38]))   For any nonsingular real projective algebraic plane curve of degree $m=2k$

$$-\frac 32k(k-1)\le p-n\le\frac 32 k(k-1)+1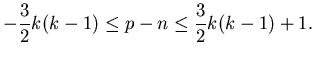.$$ (2)

(Recall that $p$ denotes the number of even ovals on the curve (i.e., ovals each of which is enveloped by an even number of other ovals, see Section 1.11), and $n$ denotes the number of odd ovals.)

As it follows from [Pet-33] and [Pet-38], Petrovsky did not know Ragsdale's paper. But his proof runs along the lines indicated by Ragsdale. He also reduced the problem to estimates of Euler characteristic of the pencil curves, but he went further: he proved these estimates. Petrovsky's proof was based on a technique that was new in the study of the topology of real curves: the Euler-Jacobi interpolation formula. Petrovsky's theorem was generalized by Petrovsky and Oleinik [PO-49] to the case of varieties of arbitrary dimension, and by Olenik [Ole-51] to the case of curves on a surface. More about the proof and the influence of Petrovsky's work on the subsequent development of the subject can be found in Kharlamov's survey [Kha-86] in Petrovsky's collected works. I will only comment that in application to nonsingular projective plane curves, the full potential of Petrovsky's method, insofar as we are able to judge, was immediately realized by Petrovsky himself.

We now turn to Gudkov's work. In a series of papers in the 1950's and 1960's, he completed the development of the techniques needed to realize Hilbert's approach to the problem of classifying curves of degree 6 (these techniques were referred to as the Hilbert-Rohn method by Gudkov), and he used the techniques to solve this problem (see [GU-69]). The answer turned out to be elegant and stimulating.

1.13.B (Gudkov's Theorem [GU-69])   The $56$ isotopy types listed in Table 4, and no others, can be realized by nonsingular real projective algebraic plane curves of degree $6$.

Table 4: Isotopy types of nonsingular real projective algebraic plane curves of degree $6$.

This result, along with the available examples of curves of higher degree, led Gudkov to the following conjectures.

1.13.C (Gudkov Conjectures [GU-69])   (i) For any M-curve of even degree $m=2k$

$$p-n\equiv k^2\quad \mod 8.$$

(ii) For any $(M-1)$-curve of even degree $m=2k$

$$p-n\equiv k^2\pm 1\quad\mod 8.$$

While attempting to prove conjecture 1.13.C(i), V. I. Arnold [Arn-71] discovered some striking connections between the topology of a real algebraic plane curve and the topology of its complexification. Although he was able to prove the conjecture itself only in a weaker form (modulo 4 rather than 8), the new point of view he introduced to the subject opened up a remarkable perspective, and in fact immediately brought fruit: in the same paper [Arn-71] Arnold proved several new prohibitions (in particular, he strengthened Petrovsky's inequalities 1.13.A). The full conjecture 1.13.C(i) and its high-dimensional generalizations were proved by Rokhlin [Rok-72], based on the connections discovered by Arnold in [Arn-71].

I am recounting this story briefly here only to finish the preliminary history exposition. At this point the technique aspects are getting too complicated for a light exposition. After all, the prohibitions, which were the main contents of the development at the time we come to, are not the main subject of this book. Therefore I want to switch to more selective exposition emphasizing the most profound ideas rather than historical sequence of results.

A reader who prefare historic exposition can find it in Gudkov's survey article [Gud-74]. To learn about the many results obtained using methods from the modern topology of manifolds and complex algebraic geometry (the use of which was begun by Arnold in [Arn-71]), the reader is referred to the surveys [Wil-78], [Rok-78], [Arn-79], [Kha-78], [Kha-86], [Vir-86].