Next: 3.4 Survey of Prohibitions
Up: 3 The Topological Point
Previous: 3.2 The Most Elementary
3.3 A Survey of Prohibitions on the Real Schemes Which Come from
Topology
In this section I list all
prohibitions on the real scheme of a flexible curve of degree 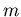 that
I am aware of, including the ones already referred to above,
but excluding prohibitions which follow from the other prohibitions
given here or from the prohibitions on the complex schemes which are
given in the next section.
that
I am aware of, including the ones already referred to above,
but excluding prohibitions which follow from the other prohibitions
given here or from the prohibitions on the complex schemes which are
given in the next section.
3.3.A
A curve is one-sided if and only if
it has odd degree.
This fact was given before as a corollary of Bézout's theorem (see
Section 1.3) and proved for flexible curves in Section
3.2 (Theorem 3.2.G).
3.3.B. Harnack's Inequality.
The number of
components of the set of real points of a curve of degree
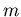
is at
most
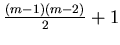
.
Harnack's inequality is undoubtedly the best known and most important
prohibition. It can also be deduced from Bézout's theorem (cf.
Section 1.3) and was proved for flexible curves in
Section 3.2 (Theorem 3.2.A).
In prohibitions 3.3.C-3.3.P the degree 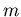 of the curve
is even:
of the curve
is even: 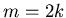 .
.
<\P>
Extremal Properties of Harnack's Inequality
<\P>
3.3.C. Gudkov-Rokhlin Congruence.
In the case of an M-curve (i.e., if
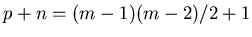
),
3.3.D. Gudkov-Krakhnov-Kharlamov Congruence.
In the case of an
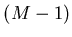
-curve (i.e., if
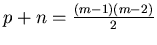
),
The Euler characteristic of a component of the complement of a curve in
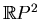 is called the characteristic of the oval which
bounds the component from outside. An oval with a positive characteristic
is said to be elliptic, an oval with the zero characteristic is
said to be parabolic and an oval with a negative characteristic
is said to be hyperbolic.
is called the characteristic of the oval which
bounds the component from outside. An oval with a positive characteristic
is said to be elliptic, an oval with the zero characteristic is
said to be parabolic and an oval with a negative characteristic
is said to be hyperbolic.
3.3.E. Fiedler's Congruence.
If the curve is an
M-curve,
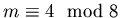
, and every even oval has an even
characteristic, then
3.3.F. Nikulin's Congruence.
If the curve is an
M-curve,
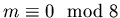
, and the characteristic of
every even oval is divisible by
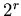
, then
where 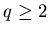 and
and
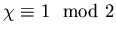 .
.
3.3.G. Nikulin's Congruence.
If the curve is an
M-curve,
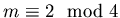
and the characteristic of
every odd oval is divisible by
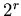
, then
Denote the number of even ovals with positive characteristic
by 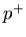 ,
the number of even ovals with zero characteristic by
,
the number of even ovals with zero characteristic by 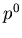 ,
and the number of even ovals with negative
characteristic by
,
and the number of even ovals with negative
characteristic by 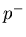 . Similarly define
. Similarly define 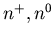 and
and 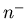 for
the odd
ovals; and let
for
the odd
ovals; and let 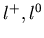 and
and 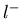 be the corresponding numbers for
both even and odd ovals together.
be the corresponding numbers for
both even and odd ovals together.
Refined Petrovsky Inequalities
Refined Arnold Inequalities
Extremal Properties of the Refined Arnold
Inequalities
3.3.L
If
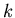
is even and
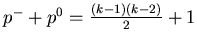
, then
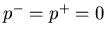
.
3.3.M
If
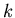
is odd and
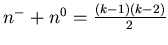
, then
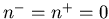
and there is only
one outer oval at all.
Viro-Zvonilov Inequalities
Besides Harnack's inequality, we know only one family of
prohibition coming from topology
which extends to real schemes of both even and odd degree. For
proofs see [VZ-92].
3.3.N. Bound of the Number of Hyperbolic Ovals.
The number of
components of the complement of a curve of odd degree
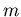
that have a
negative Euler characteristic does not exceed
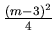
. In
particular, for any odd
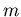
The latter inequality also holds true for even 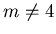 , but it
follows from Arnold inequalities 3.3.J and 3.3.K.
, but it
follows from Arnold inequalities 3.3.J and 3.3.K.
3.3.O. Bound of the
Number of Nonempty Ovals.
If
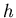
is a divisor
of
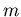
and a power of an odd prime, and if
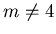
,
then
If 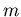 is even, this inequality follows from 3.3.J-3.3.L.
is even, this inequality follows from 3.3.J-3.3.L.



Next: 3.4 Survey of Prohibitions
Up: 3 The Topological Point
Previous: 3.2 The Most Elementary
Oleg Viro
2000-12-30
![]() of the curve
is even:
of the curve
is even: ![]() .
.
![]() is called the characteristic of the oval which
bounds the component from outside. An oval with a positive characteristic
is said to be elliptic, an oval with the zero characteristic is
said to be parabolic and an oval with a negative characteristic
is said to be hyperbolic.
is called the characteristic of the oval which
bounds the component from outside. An oval with a positive characteristic
is said to be elliptic, an oval with the zero characteristic is
said to be parabolic and an oval with a negative characteristic
is said to be hyperbolic.
![]() ,
the number of even ovals with zero characteristic by
,
the number of even ovals with zero characteristic by ![]() ,
and the number of even ovals with negative
characteristic by
,
and the number of even ovals with negative
characteristic by ![]() . Similarly define
. Similarly define ![]() and
and ![]() for
the odd
ovals; and let
for
the odd
ovals; and let ![]() and
and ![]() be the corresponding numbers for
both even and odd ovals together.
be the corresponding numbers for
both even and odd ovals together.
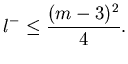
![]() , but it
follows from Arnold inequalities 3.3.J and 3.3.K.
, but it
follows from Arnold inequalities 3.3.J and 3.3.K.
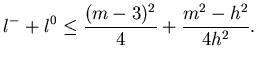
![]() is even, this inequality follows from 3.3.J-3.3.L.
is even, this inequality follows from 3.3.J-3.3.L.