


Next: 3.5 Ideas of Some
Up: 3 The Topological Point
Previous: 3.3 A Survey of
3.4 Survey of Prohibitions on the Complex Schemes
Which Come From Topology
Recall that 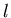 denotes
the total number of ovals on the curve. The following theorem is a
reformulation of 3.2.E.
denotes
the total number of ovals on the curve. The following theorem is a
reformulation of 3.2.E.
3.4.A. (See
2.6.A)
A curve with empty
real point set is of type II
.
3.4.C.
Rokhlin Complex Orientation Formula
(see
2.7.C))
Let
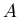
be a nonsingular
curve of type I
and degree 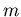 . Then
. Then
Extremal Properties of Harnack's
Inequality
3.4.E. Kharlamov-Marin Congruence.
Any
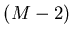
-curve of even degree
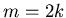
with
is of type I
.
Extremal Properties of the Refined Arnold
Inequalities
3.4.F
If
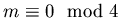
and
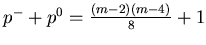
, then the curve is of type I
.
3.4.G
If
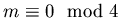
and
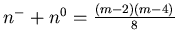
, then the curve is of
type I
.
Extremal Properties of the Viro-Zvonilov Inequality
3.4.H
Under the hypothesis of
3.3.P, the curve
is of type I
.
Congruences
3.4.I. Nikulin-Fiedler Congruence.
If
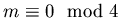
, the curve is of type I
, and every even
oval has even characteristic, then
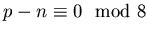 .
.
The next two congruences are included violating a general promise given
at the beginning of the previous section. There I promised exclude
prohibitions which follow from other prohibitions given here. The following
two congruences are consequences of Rokhlin's formula 3.4.C.
The first of them was discovered long before 3.4.C. The second
was overlooked by Rokhlin in [Rok-74], where he even mistakenly proved
that such a result cannot exist. Namely, Rokhlin proved that the
complex orientation formula does not imply any result which would not
follow from the prohibitions known by that time and could be
formulated solely in terms of the real scheme. Slepian congruence
3.4.K for M-curves is the only counter-example to this
Rokhlin's statement. Slepian was Rokhlin's student, he discovered a gap
in Rokhlin's arguments and deduced 3.4.K.
3.4.J. Arnold Congruence (see
2.7.D))
If
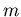
is even and the curve is of type I, then
3.4.K. Slepian Congruence.
If
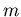
is even, the curve
is of type I
, and every odd oval has even characteristic,
then
Rokhlin Inequalities
Denote by 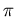 and
and 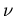 the number of even and odd nonempty ovals,
respectively, bounding from the outside those components of the
complement of the curve which have the property that each of the ovals
bounding them from the inside envelops an odd number of other ovals.
the number of even and odd nonempty ovals,
respectively, bounding from the outside those components of the
complement of the curve which have the property that each of the ovals
bounding them from the inside envelops an odd number of other ovals.
3.4.L
If the curve is of type I
and
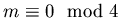 , then
, then
3.4.M
If the curve is of type I
and
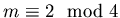 , then
, then



Next: 3.5 Ideas of Some
Up: 3 The Topological Point
Previous: 3.3 A Survey of
Oleg Viro
2000-12-30
![$\displaystyle l\equiv \left[\frac m2\right]\mod 2.$](img547.png)
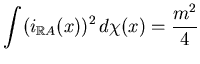
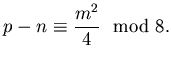
![]() and
and ![]() the number of even and odd nonempty ovals,
respectively, bounding from the outside those components of the
complement of the curve which have the property that each of the ovals
bounding them from the inside envelops an odd number of other ovals.
the number of even and odd nonempty ovals,
respectively, bounding from the outside those components of the
complement of the curve which have the property that each of the ovals
bounding them from the inside envelops an odd number of other ovals.