in contexts where this will not lead to
confusion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...crossing,2
Sometimes other names are used. For example: a
node, a point of type 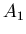 with two real branches, a nonisolated
nondegenerate double point.
with two real branches, a nonisolated
nondegenerate double point.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... pieces.3
Proof:
the closure of tne union of a connected component of
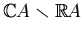 with its image under
with its image under 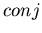 is open and close in
is open and close in
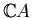 , but
, but
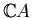 is
connected.
is
connected.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... sphere.4
I believe
that this may be assumed well-known. A short explanation
is that a projective line is a one-point compactification of an
affine line, which, in the complex case, is homeomorphic to
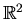 . A one-point compactification of
. A one-point compactification of
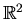 is unique up to
homeomorphism and homeomorphic to
is unique up to
homeomorphism and homeomorphic to 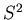 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
....5
Division
by 2 appears here to make this notion closer to the well-known
notion for an affine plane curve. In the definition for affine
situation one uses a ray instead of entire line. In the projective
situation there is no natural way to divide a line into two rays, but we
still have an opportunity to divide the result by 2. Another
distinction from the affine situation is that there the index may be
negative. It is related to the fact that the affine plane is
orientable, while the projective plane is not.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... tree6
Here by the diameter of a tree
it is understood the maximal number of edges in a simple chain of edges
of the tree, i. e., the diameter of the tree in the internal metric,
with respect to which each edge has length 1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.