


Next: 5.4 Surfaces of Low
Up: 5 Real Algebraic Spatial
Previous: 5.2 Digression: Topology of
5.3 Restrictions on Topology of Real Algebraic
Surfaces
As in the case of real plane projective curves,
the set of real points of a nonsingular spatial surface of degree 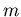 is one-sided, if
is one-sided, if 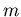 is odd, and two-sided, if
is odd, and two-sided, if 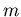 is even. Indeed, by
the Bézout theorem a generic line meets a surface of degree
is even. Indeed, by
the Bézout theorem a generic line meets a surface of degree 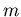 in a
number of points congruent to
in a
number of points congruent to 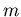 modulo 2. On the other hand, whether
a topological surface embedded in
modulo 2. On the other hand, whether
a topological surface embedded in
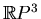 is one-sided or two-sided,
can be detected by its intersection number modulo 2 with a generic
line: a surface is one-sided, iff its intersection number with a
generic line is odd.
is one-sided or two-sided,
can be detected by its intersection number modulo 2 with a generic
line: a surface is one-sided, iff its intersection number with a
generic line is odd.
There are some other restrictions on topology of a nonsingular surface
of degree 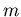 which can be deduced from the Bézout theorem.
which can be deduced from the Bézout theorem.
5.3.A. (On Number of Cubic's Components).
The set of
real points of a nonsingular surface of degree three consists of at
most two components.
Proof.
Assume that there are at least three components. Only one of
them is one-sided, the other two are contractible. Connect with a line
two contractible components. Since they are zero-homologous, the line
should intersect each of them with even intersection number. Therefore
the total number of intersection points (counted with multiplicities)
of the line and the surface is at least four. This contradicts to the
Bézout theorem, according to which it should be at most
three.

5.3.B. (On Two-Component Cubics).
If the set of real
points of a nonsingular surface of degree 3 consists of two components,
then the components are homeomorphic to the sphere and projective plane
(i. e., this is
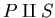
).
Proof.
Choose a point inside the contractible component. Any line
passing through this point intersects the contractible component at
least in two points. These points are geometrically distinct, since the
line should intersect also the one-sided component. On the other hand,
the total number of intersection points is at most three according to
the Bézout theorem. Therefore any line passing through the selected
point intersects one-sided component exactly in one point and two-sided
component exactly in two points. The set of all real lines
passing through the point is
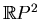
. Drawing a line through the
selected point and a real point of the surface defines a
one-to-one map of the one-sided component onto
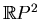
and
two-to-one map of the two-sided component onto
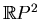
. Therefore
the Euler characteristic of the one-sided component is equal to
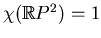
, and the Euler characteristic of the two-sided
component is
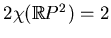
. This determines the topological types of
the components.

5.3.C. (Estimate for Diameter of Region Tree).
The
diameter of the region tree
6 of a nonsingular surface
of degree
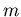
is at most
![$ [m/2]$](img55.png)
.
Proof.
Choose two vertices of the region tree the most distant from
each other. Choose a point in each of the coresponding regions
and connect the points by a line.

5.3.D
The set of real points of a nonsingular
surface of degree 4 has at most two noncontractible components. If the
number of noncontractible components is 2, then there is no other
component.
Proof.
First, assume that there are at least three noncontractible
components. Consider the complement of the union of three
noncontractible components. It consists of three domains, and at least
two of them are not adjacent (cf. the previous subsection: the graph
of adjacency of the domains should be a tree). Connect points of
nonadjacent domains with a line. It has to intersect each of the three
noncontractible components. Since they are zero-homologous, it
intersects each of them at least in two points. Thus, the total number
intersection points is at least 6, which contradicts to the Bézout
theorem.
Now assume that there are two noncontractible components and some
contractible component. Choose a point  inside the contractible
component. The noncontractible components divide
inside the contractible
component. The noncontractible components divide
 into 3
domains. One of the domains is adjacent to the both noncontractible
components, while each of the other two domains is bounded by a single
noncontractible component. If the contractible component lies in a
domain bounded by a single noncontractible component, then take a point
into 3
domains. One of the domains is adjacent to the both noncontractible
components, while each of the other two domains is bounded by a single
noncontractible component. If the contractible component lies in a
domain bounded by a single noncontractible component, then take a point
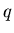 in the other domain of the same sort, and connect
in the other domain of the same sort, and connect 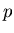 and
and 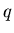 with
a line. This line meets each of the three components at least twice,
which contradicts to the Bézout theorem.
with
a line. This line meets each of the three components at least twice,
which contradicts to the Bézout theorem.
Otherwise (i. e. if the contractible component lies in the domain
adjacent to both noncontractible components), choose inside each of the
two other domains an embedded circle, which does not bound in
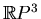 .
Denote these circles by
.
Denote these circles by 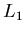 and
and 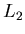 . Consider a surface
. Consider a surface 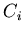 swept
by lines connecting
swept
by lines connecting 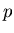 with points of
with points of 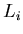 . It realizes the
nontrivial homology class. Indeed, take any line
. It realizes the
nontrivial homology class. Indeed, take any line 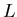 transversal to it.
Each point of
transversal to it.
Each point of 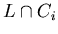 corresponds to a point of the intersection of
corresponds to a point of the intersection of
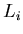 and the plane consisting of lines joining
and the plane consisting of lines joining 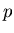 with
with 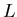 . Since
. Since
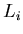 realizes the nonzero homology class, the intersection number of
realizes the nonzero homology class, the intersection number of
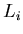 with a plane is odd. Therefore the intersection number of
with a plane is odd. Therefore the intersection number of 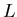 and
and
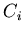 is odd. Since both
is odd. Since both 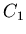 and
and 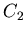 realizes the nontrivial
homology class, their intersection realizes the nontrivial
one-dimensional homology class. This may happen only if there is a
line passing through
realizes the nontrivial
homology class, their intersection realizes the nontrivial
one-dimensional homology class. This may happen only if there is a
line passing through 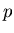 and meeting
and meeting 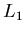 and
and 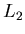 . Such a line has
to intersect all three components of the quadric surface. Each of the
components has to be met at least twice. This contradicts to the
Bézout theorem.
. Such a line has
to intersect all three components of the quadric surface. Each of the
components has to be met at least twice. This contradicts to the
Bézout theorem. 
Remark 5.3.E
In fact, if a nonsingular quartic surface has
two noncontractible components then each of them is homeomorphic to
torus. It follows from an extremal property of the
refined Arnold inequality
5.3.L. I do not know, if it can
be deduced from the Bézout theorem. However, if to assume that one
can draw lines in the domains of the complement which are not adjacent
to both components, then it is not difficult to find homeomorphisms
between the components of the surface and the torus, which is the
product of these two lines. Cf. the proof of
5.3.B.
5.3.F.
Generalization of
5.3.D.
Let
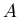
be a
nonsingular real algebraic surface of
degree
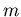
in the
3-dimensional projective space. Then the diameter of the adjacency tree
of domains of the complement
of
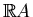
is at most
![$ [m/2]$](img55.png)
. If the degree is even
and the diameter of the adjacency tree of the connected components of
the complement of the union of the noncontractible components is
exactly
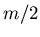
, then there is no contractible components.
The proof is a straightforward generalization of the proof of
5.3.D.
Surprisingly, Bézout theorem gave much less restrictions in the case
of surfaces than in the case of plane curves. In particular, it does
not give anything like Harnack Inequality. Most of restrictions on
topology of surfaces are analogous to the restrictions on flexible curves
and were obtained using the same topological tools. Here is a list of
the restrictions, though it is non-complete in any sense.
The restrictions are formulated below for a nonsingular real algebraic
surface 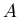 of degree
of degree 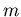 in the 3-dimensional projective space. In
these formulations and in what follows we shall denote the
in the 3-dimensional projective space. In
these formulations and in what follows we shall denote the 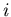 -th Betti
number of
-th Betti
number of 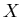 over field
over field
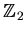 (which is nothing but
(which is nothing but
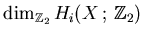 ) by
) by 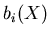 . In particular,
. In particular, 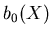 is the
number of components of
is the
number of components of 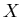 . By
. By 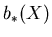 we denote the total Betti
number, i. e.
we denote the total Betti
number, i. e.
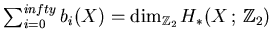 .
.
5.3.G. Generalized Harnack Inequality.
Remark 5.3.H
This is a special case of Smith-Floyd Theorem
3.2.B, which in the case of curves implies Harnack
Inequality, see Subsections
3.2. It says that
for any involution
of a topological space
Applying this to the complex conjugation involution of the
complexification
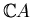
of
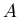
and taking into account that
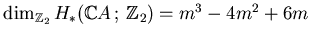
one gets
5.3.G.
5.3.I.
Extremal Congruences of Generalized Harnack
Inequality.
If
then
If
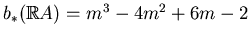 , then
, then
5.3.J. Petrovsky - Oleinik Inequalities.
Denote the numbers of orientable components of
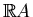 with positive,
zero and negative Euler characteristic by
with positive,
zero and negative Euler characteristic by 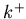 ,
, 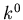 and
and 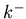 respectively.
respectively.
5.3.K.
Refined Petrovsky - Oleinik Inequality.
If
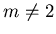
then
5.3.L Refined Arnold Inequality.
Either
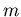
is
even,
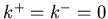
and
or


 Next: 5.4 Surfaces of Low
Up: 5 Real Algebraic Spatial
Previous: 5.2 Digression: Topology of
Oleg Viro
2000-12-30
Next: 5.4 Surfaces of Low
Up: 5 Real Algebraic Spatial
Previous: 5.2 Digression: Topology of
Oleg Viro
2000-12-30
![]() which can be deduced from the Bézout theorem.
which can be deduced from the Bézout theorem.
![]() inside the contractible
component. The noncontractible components divide
inside the contractible
component. The noncontractible components divide
![]() into 3
domains. One of the domains is adjacent to the both noncontractible
components, while each of the other two domains is bounded by a single
noncontractible component. If the contractible component lies in a
domain bounded by a single noncontractible component, then take a point
into 3
domains. One of the domains is adjacent to the both noncontractible
components, while each of the other two domains is bounded by a single
noncontractible component. If the contractible component lies in a
domain bounded by a single noncontractible component, then take a point
![]() in the other domain of the same sort, and connect
in the other domain of the same sort, and connect ![]() and
and ![]() with
a line. This line meets each of the three components at least twice,
which contradicts to the Bézout theorem.
with
a line. This line meets each of the three components at least twice,
which contradicts to the Bézout theorem.
![]() .
Denote these circles by
.
Denote these circles by ![]() and
and ![]() . Consider a surface
. Consider a surface ![]() swept
by lines connecting
swept
by lines connecting ![]() with points of
with points of ![]() . It realizes the
nontrivial homology class. Indeed, take any line
. It realizes the
nontrivial homology class. Indeed, take any line ![]() transversal to it.
Each point of
transversal to it.
Each point of ![]() corresponds to a point of the intersection of
corresponds to a point of the intersection of
![]() and the plane consisting of lines joining
and the plane consisting of lines joining ![]() with
with ![]() . Since
. Since
![]() realizes the nonzero homology class, the intersection number of
realizes the nonzero homology class, the intersection number of
![]() with a plane is odd. Therefore the intersection number of
with a plane is odd. Therefore the intersection number of ![]() and
and
![]() is odd. Since both
is odd. Since both ![]() and
and ![]() realizes the nontrivial
homology class, their intersection realizes the nontrivial
one-dimensional homology class. This may happen only if there is a
line passing through
realizes the nontrivial
homology class, their intersection realizes the nontrivial
one-dimensional homology class. This may happen only if there is a
line passing through ![]() and meeting
and meeting ![]() and
and ![]() . Such a line has
to intersect all three components of the quadric surface. Each of the
components has to be met at least twice. This contradicts to the
Bézout theorem.
. Such a line has
to intersect all three components of the quadric surface. Each of the
components has to be met at least twice. This contradicts to the
Bézout theorem. ![]()
![]()
![]() of degree
of degree ![]() in the 3-dimensional projective space. In
these formulations and in what follows we shall denote the
in the 3-dimensional projective space. In
these formulations and in what follows we shall denote the ![]() -th Betti
number of
-th Betti
number of ![]() over field
over field
![]() (which is nothing but
(which is nothing but
![]() ) by
) by ![]() . In particular,
. In particular, ![]() is the
number of components of
is the
number of components of ![]() . By
. By ![]() we denote the total Betti
number, i. e.
we denote the total Betti
number, i. e.
![]() .
.
![]() with positive,
zero and negative Euler characteristic by
with positive,
zero and negative Euler characteristic by ![]() ,
, ![]() and
and ![]() respectively.
respectively.