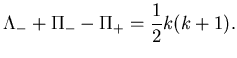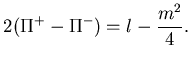
Here are Rokhlin's formulations from [Rok-78].
Theorems 2.7.A and 2.7.B can be united into a single formulation. This requires, however, two preliminary definitions.
First, given an oriented topological curve ![]() on
on
![]() , for any point
, for any point
![]() of its complement, there is the index
of its complement, there is the index ![]() of the point with
respect to the curve. It is a nonnegative integer defined as follows.
Draw a line
of the point with
respect to the curve. It is a nonnegative integer defined as follows.
Draw a line ![]() on
on
![]() through
through ![]() transversal to
transversal to ![]() . Equip it with
a normal vector field vanishing only at
. Equip it with
a normal vector field vanishing only at ![]() . For such a vector field,
one may take the velocity field of a rotation of the line around
. For such a vector field,
one may take the velocity field of a rotation of the line around ![]() .
At each intersection point of
.
At each intersection point of ![]() and
and ![]() there are two directions
transversal to
there are two directions
transversal to ![]() : the direction of the vector belonging to the normal
vector field and the direction defined by the local orientation of
: the direction of the vector belonging to the normal
vector field and the direction defined by the local orientation of ![]() at the point. Denote the number of intersection points where the
directions are faced to the same side of
at the point. Denote the number of intersection points where the
directions are faced to the same side of ![]() by
by ![]() and the number of
intersection points where the directions are faced to the opposite
sides of
and the number of
intersection points where the directions are faced to the opposite
sides of ![]() by
by ![]() . Then put
. Then put
![]() .5 It is easy to check
that
.5 It is easy to check
that ![]() is well defined: it depends neither on the choice of
is well defined: it depends neither on the choice of
![]() , nor on the choice of the normal vector field. It does not change
under reversing of the orientation of
, nor on the choice of the normal vector field. It does not change
under reversing of the orientation of ![]() . Thus for any nonsingular
curve
. Thus for any nonsingular
curve ![]() of type I on the complement
of type I on the complement
![]() , one has well
defined function
, one has well
defined function
![]() .
.
The second prerequisite notion is a sort of unusual integration:
an integration with respect to the
Euler characteristic, in which the Euler
characteristic plays the role of a measure. It is well known that the
Euler characteristic shares an important property of measures: it is
additive in the sense that for any sets ![]() ,
, ![]() such that the Euler
characteristics
such that the Euler
characteristics ![]() ,
, ![]() ,
,
![]() and
and
![]() are defined,
are defined,
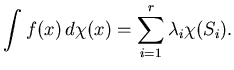
Now we can unite 2.7.A and 2.7.B:
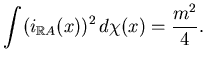
Here I give a proof of 2.7.C, skipping the most
complicated details. Take a curve ![]() of degree
of degree ![]() and type I. Let
and type I. Let
![]() be its half bounded by
be its half bounded by
![]() . It may be considered as a
chain with integral coefficients. The boundary of this chain (which is
. It may be considered as a
chain with integral coefficients. The boundary of this chain (which is
![]() equipped with the complex orientation) bounds in
equipped with the complex orientation) bounds in
![]() a chain
a chain
![]() with rational coefficients, since
with rational coefficients, since
![]() . In fact, in
the case of even degree the chain can be taken with integral
coefficients, but in the case of odd degree the coefficients are
necessarily half-integers. The explicit form of
. In fact, in
the case of even degree the chain can be taken with integral
coefficients, but in the case of odd degree the coefficients are
necessarily half-integers. The explicit form of ![]() may be given in
terms of function
may be given in
terms of function
![]() : it is a linear combination of the
fundamental cycles of the components of
: it is a linear combination of the
fundamental cycles of the components of
![]() with
coefficients equal to the values of
with
coefficients equal to the values of
![]() on the components (taken
with appropriate orientations).
on the components (taken
with appropriate orientations).
Now take the cycle
![]() and its image under
and its image under ![]() , and calculate
their intersection number in two ways.
, and calculate
their intersection number in two ways.
First, it is easy to see
that the homology class ![]() of
of
![]() is equal to
is equal to
![]() . Indeed,
. Indeed,
![]() , and therefore
, and therefore
![]() .
On the other hand,
.
On the other hand, ![]() acts in
acts in
![]() as
multiplication by
as
multiplication by ![]() , and hence
, and hence
![]() .
Therefore
.
Therefore
![]() .
.
Second, one may calculate the same intersection number geometrically:
moving the cycles into a general position and counting the local
intersection numbers. I will perturb the cycle
![]() . First,
choose a smooth tangent vector field
. First,
choose a smooth tangent vector field ![]() on
on
![]() such that it has
only nondegenerate singular points, the singular points are outside
such that it has
only nondegenerate singular points, the singular points are outside
![]() , and on
, and on
![]() the field is tangent to
the field is tangent to
![]() and directed
according to the complex orientation of
and directed
according to the complex orientation of ![]() which comes from
which comes from
![]() .
The latter means that at any point
.
The latter means that at any point
![]() the vector
the vector
![]() is directed inside
is directed inside
![]() (the multiplication by
(the multiplication by ![]() makes a
real
vector normal to the real plane and lieves any vector tangent to
makes a
real
vector normal to the real plane and lieves any vector tangent to
![]() tangent to
tangent to
![]() ). Now shift
). Now shift
![]() inside
inside
![]() along
along
![]() and extend this shift to a shift of the whole chain
and extend this shift to a shift of the whole chain ![]() along
along
![]() . Let
. Let ![]() denote the result of the shift of
denote the result of the shift of ![]() and
and ![]() denote the part of
denote the part of
![]() which was not swept during the shift. The
cycle
which was not swept during the shift. The
cycle ![]() represents the same homology class
represents the same homology class ![]() as
as
![]() ,
and we can use it to calculate the intersection number
,
and we can use it to calculate the intersection number
![]() . The cycles
. The cycles ![]() and
and
![]() intersect only at singular points of
intersect only at singular points of ![]() . At a singular point
. At a singular point ![]() they
are smooth transversal two-dimensional submanifolds, each taken with
multiplicity
they
are smooth transversal two-dimensional submanifolds, each taken with
multiplicity
![]() . The local intersection number at
. The local intersection number at ![]() is
equal to
is
equal to
![]() multiplied by the local intersection number
of the submanifolds supporting the cycles. The latter is equal to the
index of the vector field
multiplied by the local intersection number
of the submanifolds supporting the cycles. The latter is equal to the
index of the vector field ![]() at
at ![]() multiplied by
multiplied by ![]() .
.
I omit the proof of the latter statement. It is nothing but a
straightforward checking that multiplication by ![]() induces
isomorphism between tangent and normal fibrations of
induces
isomorphism between tangent and normal fibrations of
![]() in
in
![]() reversing orientation.
reversing orientation.
Now recall that the sum of indices of a vector field tangent to the
boundary of a compact manifold is equal to the Euler characteristic of
the manifold. Therefore the input of singular points lying in a
connected component of
![]() is equal to the Euler
characteristic of the component multiplied by
is equal to the Euler
characteristic of the component multiplied by
![]() for any
point
for any
point ![]() of the component. Summation over all connected components of
of the component. Summation over all connected components of
![]() gives
gives
![]() .
Its equality to the result of the first
calculation is the statement of 2.7.C.
.
Its equality to the result of the first
calculation is the statement of 2.7.C.![]()

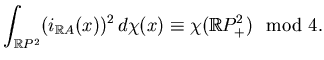
Denote the number of all injective pairs of ovals for a curve under
consideration by ![]() .
.