Patchworking Harnack Curves

In each area of mathematics there are objects which appear much more frequently than other ones. Some of them (like Dynkin diagrams) appear in several domains quite distant from each other. In topology of real plane algebraic curves Harnack curves play this role. It was not an accident that they were constructed in the first paper devoted to this subject. Whenever one tries to construct an M-curve, the first success provides a Harnack curve. Patchwork construction is no exception to the rule.

In this section we describe, using the Patchwork Theorem, the construction of some Harnack curves of an even degree $m = 2k$.

In what follows all the triangulations satisfy an additional assumption: they are primitive which means that all triangles are of area 1/2 (or, equivalently, that all integer points of the triangulated area are vertices of the triangulation). A polynomial defining a T-curve contains the maximal collection of nonzero monomials if and only if the triangulation used in the construction of the T-curve is primitive.

A primitive convex triangulation of $T$ is said to be equipped with a Harnack distribution of signs if:

vertex $(i,j)$ has the sign "-", if $i,j$ are both even, and has the sign "+" in the opposite case.

A vertex $(i,j)$ of a triangulation of $T$ is called even if $i,j$ are both even, and odd if not.

Figure 6: The real scheme of the simplest Harnack curve of degree $2k$.

Proposition 7   Patchworking applied to an arbitrary primitive convex triangulation of $T$ with the Harnack distribution of signs produces an M-curve with the real scheme shown in Figure 6.

An example of the construction under consideration is shown in Figure 7.

Figure 7: Patchwork of the simplest Harnack curve of degree 10.

Proof of Proposition. First, remark that the number of interior (i. e., lying in the interior of the triangle $T$) integer points is equal to $\frac{(m - 1)(m - 2)}{2}$, the number of even interior points is equal to $\frac{(k - 1)(k - 2)}{2}$, and the number of odd interior points is equal to $\frac{3k(k - 1)}{2}$.

Take an arbitrary even interior vertex of a triangulation of the triangle $T$. This vertex has the sign "-". All adjacent vertices (i.e. the vertices connected with the vertex by edges of the triangulation) are odd, and thus they all have the sign "+". This means that the star of an even interior vertex contains an oval of the curve $L$. The number of such ovals is equal to $\frac{(k - 1)(k - 2)}{2}$.

Take now an odd interior vertex of the triangulation. It has the sign "+". There are two vertices with "-" and one vertex with "+" among the images of the vertex under $s= s_x \circ s_y$ and $s_x,\; s_y$ (recall that $s_x,\; s_y$ are reflections with respect to the coordinate axes). Consider the image with the sign "+". It is easy to verify, that all its adjacent vertices have the sign "-". Again this means that the star of this vertex contains an oval of the curve $L$. The number of such ovals is equal to $\frac{3k(k - 1)}{2}$.

Thus

$$\frac{(k - 1)(k - 2)}{2} \; + \; \frac{3k(k-1)}{2} \; = \; \frac{(m - 1)(m - 2)}{2}$$

so the curve can only have one more oval. This oval exists, because, for example, the curve $L$ intersects the coordinate axes.

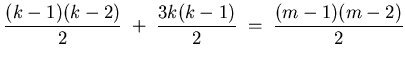
To finish the proof, we need only note that the union of the segments

$$\{x - y = -m, \; -m \leq x, y \leq m\} \;\; \cup$$

$$\{x \leq 0, \; y = 0, \; -m \leq x, y \leq m\} \;\; \cup \;\; \{x = 0, \; y \leq 0, \; -m \leq x, y \leq m\}$$

is not contractible in $\mathcal{T}$ and contains only minuses. This means that $\frac{3k(k - 1)}{2}$ ovals corresponding to odd interior points and encircling pluses are situated outside of the nonempty oval. $\qedsymbol$

ARRAY(0x8cc51c0)