3.7 Sharpness of the Inequalities

The arsenal of constructions in Section 1 and the supply of curves constructed there, which are very modest from the point of view of classification problems, turn out to be quite rich if we are interested in the problem of sharpness of the inequalities in Section 3.3.

The Harnack curves of even degree $m$ with scheme

$$\langle (3m^2-6m)/8\amalg 1 \langle m^2-6m+8)/8\rangle\rangle$$

which were constructed in Section 1.6 (see also Section 1.9) not only show that Harnack's inequality 3.3.B is the best possible, but also show the same for the refined Petrovsky inequality 3.3.H.

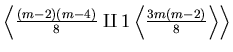One of the simplest variants of Hilbert's construction (see Section 1.10) leads to the construction of a series of M-curves of degree $m\equiv 2\mod 4$ with scheme $\left\langle \frac{(m-2)(m-4)}8\amalg1\left\langle \frac{3m(m-2)}8\right\rangle\right\rangle$. This proves that the refined Petrovsky inequality 3.3.I for $m\equiv 2\mod 4$ is sharp. If $m\equiv 0\mod 4$, the methods of Section 1 do not show that this inequality is the best possible. Nonetheless, this is true, see [Vir-80].

The refined Arnold inequality 3.3.J is best possible for any even $m$. If $m\equiv 2\mod 4$, this can be proved using the Wiman M-curves (see the end of Section 1.12). If $m\equiv 0\mod 4$, it follows using curves obtained from a modification of Wiman's construction: the construction proceeds in exactly the same way, except that the opposite perturbation is taken, as a result of which one obtains a curve that can serve as the boundary of a tubular neighborhood of an M-curve of degree $m/2$.

The last construction (doubling), if applied to an M-curve of odd degree, shows that the refined Arnold inequality 3.3.K is the best possible for $m\equiv 2\mod 4$. If $m\equiv 0\mod 4$, almost nothing is known about sharpness of the inequality 3.3.K, except that for $m=8$ the right side can be lowered by 2.