4.4 Curves of Degree 7

In this section Theorem 3.8.G is proved, i.e. it is proved that there is no nonsingular curve of degree 7 with real scheme $\langle J\amalg 1\langle14\rangle\rangle$.

Assume the contrary: suppose that there exists a nonsingular curve $X$ of degree 7 with real scheme $\langle J\amalg 1\langle14\rangle\rangle$.

Being an M-curve, $X$ is of type I (see 2.6.B) and, hence, has a complex orientation.

4.4.A. Lemma.   $X$ cannot have a complex scheme distinct from $\langle J\amalg 1^+\langle 6^+\amalg 8^-\rangle \rangle _I^7$.

Proof. Let $\varepsilon$ be the sign of the outer oval, i.e.

$$\varepsilon =\begin{cases}+1,&\text{ if the outer oval is positive}\\ -1,&\text{ otherwise.}\end{cases}$$

It is clear that

$$\Lambda ^+=\begin{cases}\Pi^-+1,&\text{ if $\varepsilon =+1$} ... ...xt{ if $\varepsilon =+1$}\\ \Pi^-+1,&\text{ if $\varepsilon =-1$}.\end{cases}$$

Therefore, $\Lambda ^+-\Lambda ^-=\varepsilon (\Pi^-+1-\Pi^+)$. On the other hand, by 2.7.B, $\Lambda ^+-\Lambda ^-=2(\Pi^-\Pi^+)+3$. From these two equalities we have

$$\varepsilon =2+\frac{1}{\Pi^-+1-\Pi^+}$$

and, since $\vert\varepsilon \vert=1$, it follows that $\varepsilon =+1$ and $\Pi^-+1-\Pi^+=-1$, i.e. $\Pi^+-\Pi^-=2$. Finally, since $\Pi^++\Pi^-=14$, it follows that $\Pi^+=8$ and $\Pi^-=6$. This gives the desired result. $\qedsymbol$

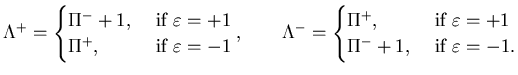
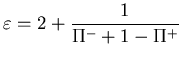
The next ingredient in the proof of Theorem 3.8.G is a kind of convexity in disposition of interior ovals. Although we study a projective problem, it is possible to speak about convexity, if it is applied to interior ovals. The exact sense of this convexity is provided in the following statement.

4.4.B. Lemma.   Let $A$ be any nonsingular curve of degree 7 with real scheme $\langle J\amalg \alpha \amalg1\langle\beta \rangle\rangle$ and the number of ovals $\ge6$. Then for each of $\beta$ interior ovals there exists a pair of real lines $L_1$, $L_2$ intersecting inside this oval such that the rest $\beta -1$ interior ovals lie in one of three domains into which $\mathbb{R}L_1\cup\mathbb{R}L_2$ cut the disk bounded by the exterior oval.

Proof. A line intersecting two interior ovals cannot intersect any other interior oval. Furthermore, it intersects each of these two interior ovals in two points, meets the nonempty oval in two points and the one-sided component in one point. (This follows from the following elementary arguments: the line intersects the one-sided component with odd multiplicity, it has to intersect the nonempty oval, since it intersects ovals inside of it, it can intersect any oval with even multiplicty and by Bézout theorem the total number of ontersection points is at most 7.) The real point set of the line is divided by the intersection points with the nonempty oval into two segments. One of these segments contains the intersection point with the one-sided component, the other one is inside the nonempty oval and contains the intersections with the interior ovals. A smaller segment connects the interior ovals inside the nonempty ovals. Thus any points inside two interior ovals can be connected by a segment of a line inside the exterior nonemty oval. See Figure 29.

Choose a point inside each interior oval and connect these points by segments inside the exterior oval. If the lines guaranteed by 4.4.B exist, then the segments comprise a convex polygon. Otherwise, there exist interior ovals $u_0$, $u_1$, $u_2$ and $u_3$ such that $u_0$ is contained inside the triangle made of the segments connecting inside the exterior oval the points $q_1$, $q_2$, $q_3$ chosen inside $u_1$, $u_2$ and $u_3$. See Figure 30.

To prove that this is impossible, assume that this is the case and construct a conic $K$ through $q_1$, $q_2$, $q_3$, the point $q_0$ chosen inside $u_0$ and a point $q_4$ chosen inside some empty oval $u_4$ distinct from $u_0$, $u_1$, $u_2$ and $u_3$ (recall that the total number of ovals is at least 6, thereby $u_4$ exists). Since the space of conics is a 5-dimensional real projective space and the conics containing a real point form a real hyperplane, there exists a real conic passing through any 5 real points. If the conic happened to be singular, we could make it nonsingular moving the points. However it cannot happen, since then the conic would be decomposed into two lines and at least one of the lines would intersect with 3 empty ovals and with the nonempty oval, which would contradict the Bézout theorem.

Now let us estimate the number of intersection points of the conic and the original curve $A$ of degree 7. The conic $\mathbb{R}K$ passes through the vertices of the triangle $q_1q_2q_3$ and through the point $q_0$ inside it. The component of the intersection of $\mathbb{R}K$ with the interior of the triangle has to be an arc connecting two points of $q_1$, $q_2$, $q_3$. Let they be $q_1$ and $q_2$. Then the segment $[q_0,q_3]$ lies outside the disk bounded by $\mathbb{R}K$. This segment together with an arc $q_0,q_1,q_3$ of $\mathbb{R}K$ is a one-sided circle in $\mathbb{R}P^2$, which has to intersect the one-sided component of $\mathbb{R}A$. Since neither the segment nor the arc $q_0,q_1$ intersect $\mathbb{R}A$, the arc $q_1,q_3$ does intersect. The intersection point is outside the nonempty oval, while both $q_1$ and $q_3$ are inside. Therefore the same arc has at least 2 common points with the nonempty oval. Similar arguments show that the arc $q_2,q_3$ intersects the one-sided component of $\mathbb{R}A$ and has at least 2 common points with the nonempty oval. Thus $\mathbb{R}K$ intersects the one-sided component of $A$ at least in 2 points and the nonempty oval at least in 4 points. See Figure 31. Together with 10 intersection points with ovals $u_i$, $i=0,1,\dots,4$ (2 points with each) it gives 16 points, which contradicts the Bézout theorem. - $(^{\arabic{endnotectr}})$endnoteii Another version of the same argument may be based on the following Lemma:

Lemma on auxiliary conics.  Let $q_0$, $q_1$, $q_2$, $q_3$ be points situated inside the outer oval of $A$ such that $q_0$ lies inside the triangle with vertices $q_1$, $q_2$, $q_3$, which is enveloped by the outer oval, and extension of each side of this triangle intersects the nonempty oval in two points and the one-sided component in one point. Then any nonsingular conic passing through $q_0$, $q_1$, $q_2$, $q_3$ intersects the nonempty oval at least in 4 points and the one-sided component at least in 2 points.

Figure 32:

Proof. Choose a coordinate system such that the points $q_0$, $q_1$, $q_2$, $q_3$ have at this system coordinates $(1:1:1)$, $(1:0:0)$, $(0:1:0)$ and $(0:0:1)$. Perform the standard triangle transformation defined by formula $(x_0:x_1:x_2)\mapsto(x_1x_2: x_0x_2:x_0x_1)$. Under this transformation the one-sided component turns to an oval passing through $q_1$, $q_2$, $q_3$. The nonempty oval turns to a curve with nondegenerate double points at $q_1$, $q_2$, $q_3$, which goes twice around the triangle $q_1q_2q_3$, "f123d" and looks like a standard projection of trefoil (see Figure 32). The non-singular conic passing through $q_0q_1q_2q_3$ turns to a line which passes through $q_0$ and contains none of $q_1$, $q_2$, $q_3$. It is clear that such a line has to intersect the images of the one-sided component and the nonempty oval at least in two and four points. This proves Lemma.$\qedsymbol$

$\qedsymbol$

Proof. [End of Proof of Theorem 3.8.G] Assume that a curve $X$ prohibited by Theorem 3.8.G does exist. According to Lemma 4.4.A, its complex scheme is $\langle J\amalg 1^+\langle 6^+\amalg 8^-\rangle \rangle _I^7.$ Take a point inside a positive interior oval. Consider the segment of the pencil of line passing through this point. The other interior ovals compose a chain. By Lemma 4.4.B they lie in one connected component of the intersection of the domain swept by the lines of the segment of the pencil with the interior domain of the nonempty oval. By Theorem 4.2.C signs of ovals in this chain alternate. Therefore the difference between the numbers of positive and negative ovals is 1, while it has to be 3 by Lemma 4.4.A. $\qedsymbol$