- 1.1 Basic Definitions and Problems
- 1.2 Digression: the Topology of Closed One-Dimensional Submanifolds of the Projective Plane
- 1.3 Bézout's Prohibitions and the Harnack Inequality
- 1.4 Curves of Degree
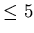
- 1.5 The Classical Method of Constructing Nonsingular Plane Curves
- 1.6 Harnack Curves
- 1.7 Digression: the Space of Real Projective Plane Curves
- 1.8 End of the Proof of Theorem 1.6.A
- 1.9 Isotopy Types of Harnack M-Curves
- 1.10 Hilbert Curves
- 1.11 Analysis of the Results of the Constructions. Ragsdale
- 1.12 Generalizations of Harnack's and Hilbert's Methods. Brusotti. Wiman
- 1.13 The First Prohibitions not Obtained from Bézout's Theorem
- Exercises
- 2.1 Complex Topological Characteristics of a Real Curve
- 2.2 The First Examples
- 2.3 Classical Small Perturbations from the Complex Point of View
- 2.4 Further Examples
- 2.5 Digression: Oriented Topological Plane Curves
- 2.6 The Simplest Restrictions on a Complex Scheme
- 2.7 Rokhlin's Complex Orientation Formula
- 2.8 Complex Schemes of Degree
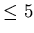
- Exercises
- 3.1 Flexible Curves
- 3.2 The Most Elementary Prohibitions on Real Topology of a Flexible Curve
- 3.3 A Survey of Prohibitions on the Real Schemes Which Come from Topology
- 3.4 Survey of Prohibitions on the Complex Schemes Which Come From Topology
- 3.5 Ideas of Some Proofs
- 3.6 Flexible Curves of Degrees
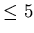
- 3.7 Sharpness of the Inequalities
- 3.8 Prohibitions not Proven for Flexible Curves